
The 421 polytope has 6720
edges.
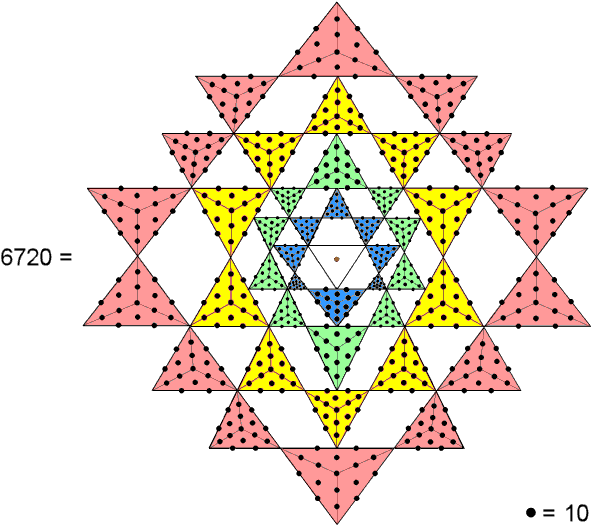
Constructed from Type A triangles, the 2-d Sri Yantra embodies the number 6720 when each extra yod is assigned the number 10.
| << Previous 1... 14 15 [16] 17 18 ...24 Next >> |
16. The 2-d Sri Yantra embodies the number of edges of the 421 polytope
 |
 |
|
|
Constructed from Type A triangles, the 2-d Sri Yantra embodies the number 6720 when each extra yod is assigned the number 10. |
A Type A triangle contains 19 yods. Of these, three are corners, so that 16 more yods are needed to turn a simple
triangle into a Type A triangle. The 42 triangles surrounding the centre of the 2-d Sri Yantra contain (42×16=672)
yods other than their 68 corners when they are Type A triangles. In other words, 672 more yods are
needed to transform the 42 triangles into Type A triangles. When each yod is weighted with the number 10 (Decad),
the 2-d Sri Yantra embodies the number 6720. This is the number of edges in the 421 polytope.
Although traditionally regarded as a triangle, the central, downward-pointing, three-sided figure is not, from a pure mathematical point of view, a triangle because the bindu symbolising the Absolute is assigned to its centre in the case of the 2-d Sri Yantra. For this reason, it is not legitimate to treat this figure as a Type A triangle on the same par as the 42 triangles that surround it.
Of the 672 yods in the 42 Type A triangles, 42 are corners of tetractyses, leaving 630 hexagonal yods. The number 630 is the number value of Seraphim, the Order of Angels assigned to Geburah.
| << Previous 1... 14 15 [16] 17 18 ...24 Next >> |