Home

14. Pentagramic representation of the geometrical composition of the 4₂₁ polytope

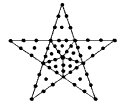
The simplest construction of the pentagram from tetractyses requires 61 yods:

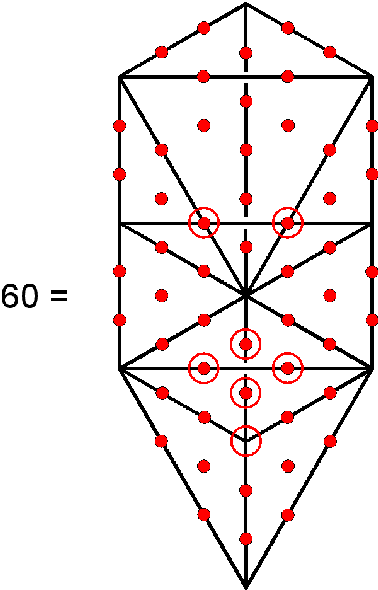
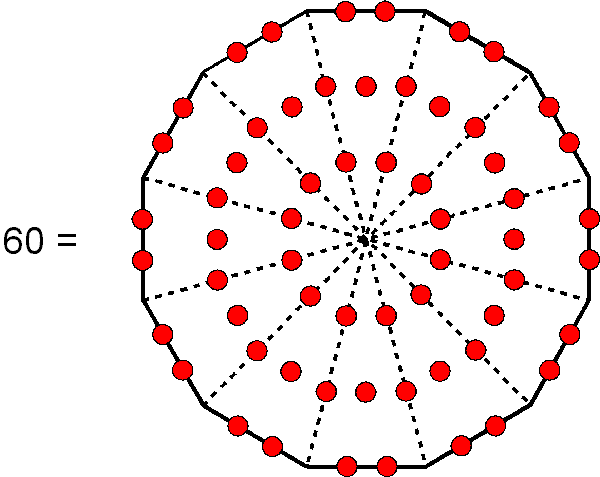
As this is the same number of yods as that present in the Type B square, all the Type B square representations of various parameters of the 4₂₁ polytope and the UPA shown above can be replaced by pentagrams constructed from tetractyses whose yods are similarly weighted. Both geometric figures express the number 60, which is a parameter of holistic systems, being, for example, the number of hexagonal yods in the Tree of Life:

and the number of hexagonal yods in the Type A dodecagon:

The next level of construction of the pentagram from Type A triangles with 19 yods requires 151 yods because each point of the star then has 15 yods outside its base, whilst the Type B pentagon has 76 yods, so that the pentagram contains (76 + 5×15 = 151) yods. Enclosed in a square, it reproduces the number value 155 of ADONAI MELEKH, the complete Godname of Malkuth. Alternatively, three nested pentagrams enclosed in a square also constitute a representation of this Godname:

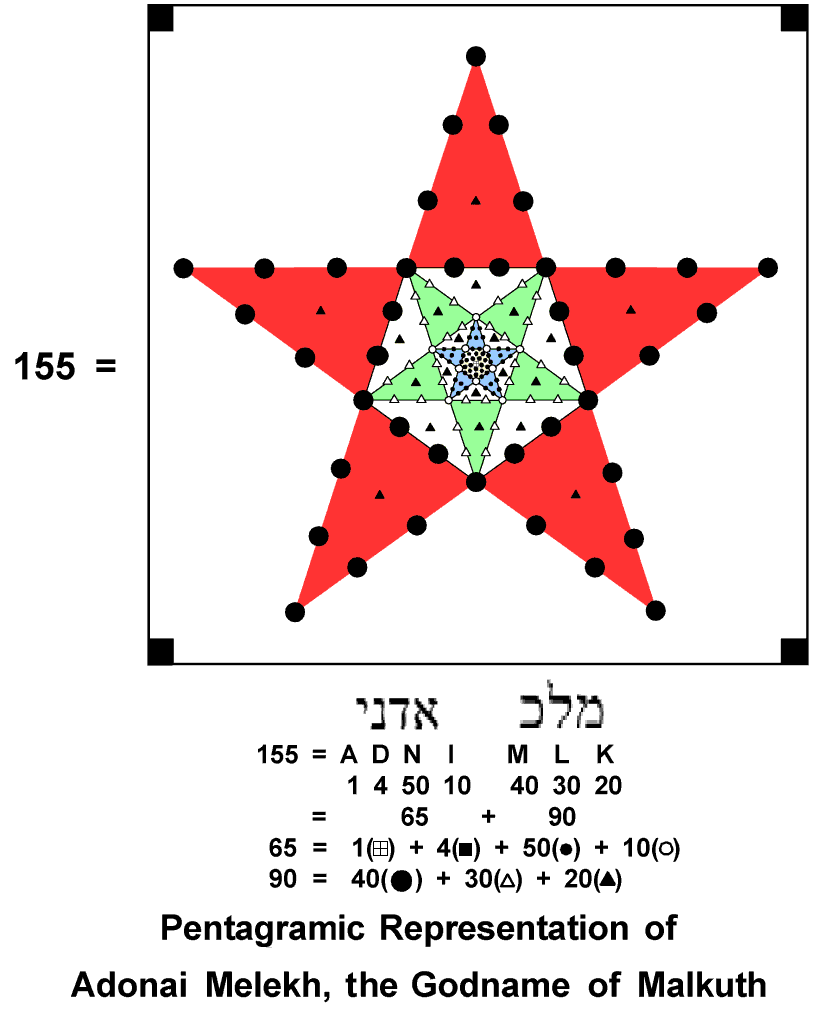
We found in #12 that the number of vertices, sides and triangles in the faces and interior of the 4₂₁ polytope = 74400 = 310×240 = 155×480. Assigning the number 480 (the number of roots of E₈×E₈) to the 155 yods generates the number of points, lines & triangles making up this polytope. As 74400 = 31×2400, this number is the number 31 of EL, the Godname of Chesed, multiplied by the 2400 space-time components of the 240 gauge fields associated with the 240 roots of E₈, as represented in 8-dimensional space by the vertices of the 4₂₁ polytope. As 2400 = 160×15 = 16×10×15, 74400 = 31×16×10×15 = 4960×15. This means that the number of points, lines & triangles in the 4₂₁ polytope is the product of the number 15 of YAH (the shortened version of YAHWEH, the Godname of Chokmah) and the number of space-time components of the 496 gauge fields that transmit superstring forces free of quantum anomalies. As

1² + 2² + 3² + ... + 15² = 496×5/2,

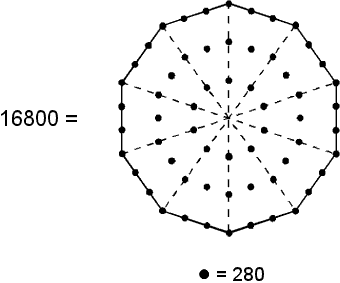
74400 = 496×150 = 60×(1²+2²+3²+...+15²). Assigning the sum of the squares of the first 15 integers to each of the 60 hexagonal yods in the Tree of Life (see above) generates the number of points, lines & triangles in the 4₂₁ polytope. This is a beautiful, mathematical property, simply connecting the geometry of the Tree of Life to the geometry of the equally archetypal 4₂₁ polytope expressing the physics of one of the two types of heterotic superstrings. As 60 yods surround the centre of the Type A decagon, assigning the sum of these squares to each yod generates the number 74400. A Type B decagon has 150 yods surrounding its centre. Assigning the number 496 of Malkuth (the crucial dimension of a Lie group that can describe anomaly-free, superstring interactions) to these yods generates the number of points, lines & lines in the 4₂₁ polytope. These results demonstrates the power of the Decad in expressing how many points, lines & triangles are needed to construct the 4₂₁ polytope. It also expresses the 16800 turns in the 10 helical whorls of the UPA because, weighted with the number 280 of Sandalphon, the Archangel of Malkuth, the 60 yods surrounding the centre of the Type A decagon generate this number:

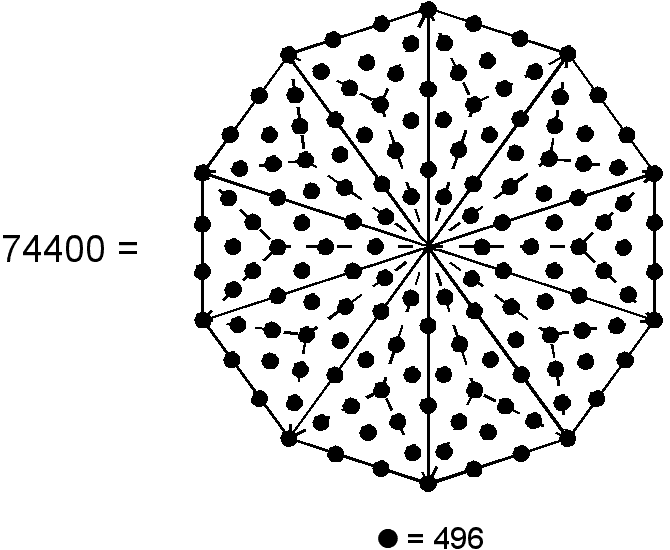Weighted with the number 280 of Sandalphon, the Archangel of Malkuth, the 60 yods surrounding the centre of the Type A decagon generate the superstring structural parameter 16800.	Weighted with the number 496 of Malkuth, the 150 yods surrounding the centre of the Type B decagon generate the number of points, lines & triangles in the 421 polytope whose 240 vertices determine the roots of the superstring symmetry group E8.

<< Previous    1...   12  13  [14]  15  16  ...24    Next >>

Home