Home

10. The correspondence between the 24-cell and the seven separate Type B polygons 

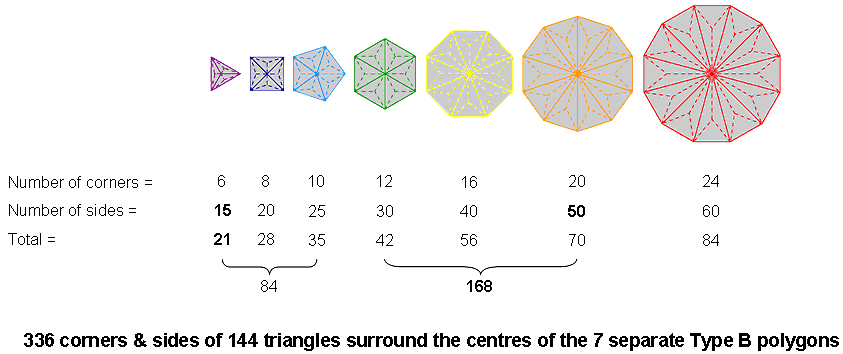
The number of corners, sides & triangles in a Type B n-gon = 10n + 1, where "1" denotes its centre. The number of corners = 2n. The number of sides = 5n. The number of triangles = 3n. The number of corners & sides = 7n. The number of corners & sides of the 144 triangles surrounding the centres of the seven Type B polygons with 48 corners = ∑7n = 7∑n = 7×48 = 336:

They comprise 96 corners and 240 sides, the latter being a parameter of holistic systems that manifests in the 24-cell as its 240 vertices, edges, faces & octahedral cells. This demonstrates par excellence the holistic character of the number 336, in particular, the Tree of Life nature of the 24-cell, which is composed of 336 geometrical elements. The seven polygons can be divided into two sets in two possible ways so as to generate the 168:168 division that other sacred geometries exhibit:

triangle+square+pentagon+dodecagon + hexagon+octagon+decagon

triangle+pentagon+hexagon+decagon + square+octagon+dodecagon

Each set displays the 24:24 division of the 48 corners of the seven polygons, a division that is also part of the universal pattern displayed by holistic systems (e.g., the 24 Yang lines and 24 Yin lines of the eight diagonal hexagrams in the 8×8 square array of 64 hexagrams). One of the combinations in either possibility displays the further 84:84 division exhibited by sacred geometries that embody the holistic parameter 168. The numbers of the types of geometrical elements in the 24-cell are: 24, 96, 96, 24 & 96. As none of them is divisible by 7 (the number of corners & sides per sector of a polygon), nor any combination thereof, no subset of polygons can have a number of corners & sides equal to any of these numbers. This means that each of the numbers characterising the geometry of the 24-cell must correspond to either all corners, all sides or partial combinations of both. Given that all these numbers are integer multiples of 24 — the number of sectors of each set of polygons — it seems natural to associate the two sets of polygons, each with 168 corners & sides, with the two halves of the 24-cell, each having 168 geometrical elements. Indeed, sacred geometries embodying the number 336 always have two "halves" (not necessarily physical), each embodying this number; the 168 turns in a half-revolution of a whorl of the UPA are the superstring example of this fundamental division. However, this leads to a problem, namely, neither possibility shown above has both sets comprising polygons with 12 corners and 12 sides to match the 12 vertices and 12 internal sides in each half of the 24-cell. The 24 vertices and 24 internal sides in the 24-cell can, therefore, correspond only to the two sets of 24 corners of the polygons, whilst its 96 edges correspond to the 96 sides of the sectors, its 96 faces correspond to the 96 sides that end on corners of polygons and its 96 internal triangles correspond to the 48 other corners and 48 sides of triangles that join to the centres of polygons. Remember that, in comparing two holistic systems, like does not have to correspond quantitatively to like. Indeed, this is, rarely, the case. All that is necessary in demonstrating their equivalence is to show the same pattern of numbers of geometrical elements. It is only that which counts, not what the numbers denote.

<< Previous    1...   8  9  [10]  11  12  ...24    Next >>

Home