Home

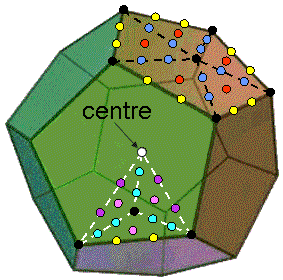
The table in Sacred geometry/Platonic solids indicates that there are 550 hexagonal yods in either the sectors of the faces of the dodecahedron constructed from tetractyses or its internal triangles divided into their sectors. The table calls Platonic solids "Type A" if they have tetractyses as internal triangles and "Type B" if their internal triangles are divided into their sectors. Regarded by Plato as the representation of the celestial sphere because, of all the five regular polyhedra, it most approximates the perfect sphere, the dodecahedron embodies the number 550 as one of the defining parameters of holistic systems, of which this mathematically complete set of 3-dimensional, regular polyhedra is an example. There are 240 hexagonal yods in its 12 faces and 310 (=31×10) hexagonal yods in its interior. The counterparts of these in the 550 yods making up the root edge and the (7+5) regular polygons encoding CTOL are the 240 hexagonal yods in one set of seven polygons and the remaining 310 yods in the root edge and all 12 polygons (see here). The dodecahedron has 12 faces with 20 vertices & 30 edges, so that its (12×5 + 30×3 = 150 = 15×10) tetractyses have (20+12+30=62) corners surrounding its centre, where 15 is the number value of YAH, the (older) Godname of Chokmah, and 62 is the number value of Tzadkiel, the Archangel of Chesed (see here), and the 31st even integer. The dodecahedron has (20+12=32) vertices & faces, where 32 is the 31st integer after 1. These properties clearly demonstrate how the Godname EL ("God") of Chesed with number value 31 prescribes the Platonic solid that represents the completion of the sequence of regular polyhedra. EL also prescribes all five solids because, starting with their 50 vertices as unconnected points in space, (50+90+180=320=32×10) more points & lines are needed to construct their 50 faces with 50 centres, 90 edges & 180 sides of sectors, 32 being the 31st integer after 1. Alternatively, 310 (=31×10) points & lines in their faces surround axes that join pairs of vertices diametrically opposite each other and pass through the centres of the polyhedra.

The table in Sacred geometry/Platonic solids also indicates that the five Platonic solids have 910 (=91×10) hexagonal yods when they are Type A. This number is the number of hexagonal yods inside the five Platonic solids when they are Type B. They embody not only the 550 SLs of the Cosmic Tree of Life (CTOL) as the 550 geometrical elements in their faces but also its 91 Trees of Life. This, again, is not a coincidence, because all representations of holistic systems are characterized by the same set of defining parameters, such as 550 & 91.

Each half of the dodecahedron contains (550/2=275) hexagonal yods. Given that either half comprises 10 vertices, 15 edges & 6 pentagonal faces, the various types of these yods are shown below:

Each half of the dodecahedron has:

There are 20 violet hexagonal yods on the 10 sides of internal triangles that join the centre of the dodecahedron to the 10 vertices in each half of it. There are (275+20=295) hexagonal yods either in the lower half or on sides joining the centre to the 20 vertices. This leaves 255 hexagonal yods in the upper half that do not line internal sides joining the centre to vertices.

295 = 20 + 20 + 60 + 30 + 30 + 90 + 45.

255 = 60 + 30 + 30 + 90 + 45.

Suppose that the dodecahedron is orientated so that its vertical axis passes through its centre and two diametrically opposite vertices. Then two violet hexagonal yods lie on each half of the axis, which is surrounded by (9+9=18) vertices, so that the number of violet hexagonal yods in its lower half is:

20 = 2 + (9×2=18).

Therefore,

295 = 2 + 18 + 45 + 20 + 60 + 30 + 30 + 90

      = (2+45) + (20+60) + (18+30+30+90)

= 47 + 80 + 168,

where

47 = 2 + 45,

80 = 20 + 60,

and

168 = (18+30+30) + 90 = 78 + 90.

 There are:

• 47 hexagonal yods either on the lower half of the axis or at centres of tetractyses in the 15 Type A triangles inside the lower half of the dodecahedron. They correspond to the 47 SLs in the 7-tree that maps the seven subplanes of the physical plane (see previous page);
• (80+168=248) more hexagonal yods in the lower half. 80 is the number value of Yesod, 248 is the number value of Raziel, the Archangel of Chokmah, and 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. The number value 78 of Cholem is the number of red (30), yellow (30) & violet (18) hexagonal yods in the lower half of the dodecahedron that surround its axis; the number value 90 of Yesodoth is the number of turquoice hexagonal yods in this half:

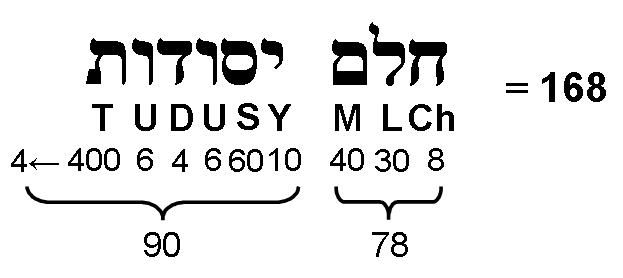
The 248 hexagonal yods correspond to the 248 SLs above the 7-tree as far as Chesed of the 49th Tree mapping the highest subplane of the seventh plane. The 80:168 division of 248 is characteristic of holistic systems embodying the number 248 as the dimension of E₈, the rank-8, exceptional Lie group that plays a central role in E₈×E₈ heterotic superstring theory. For example, it shows up in the way the Godname EL prescribes this number in five overlapping Trees of Life (see here).

• 255 hexagonal yods in the upper half of the dodecahedron that do not line sides joining vertices to its centre; they correspond to the 255 SLs above Chesed of the 49th Tree (295th SL) up to the top of CTOL. The unique nature of this SL is that it is the first Sephirah of Construction of the first Tree of Life expressing this Sephirah in the 49 Trees that map the cosmic physical plane.

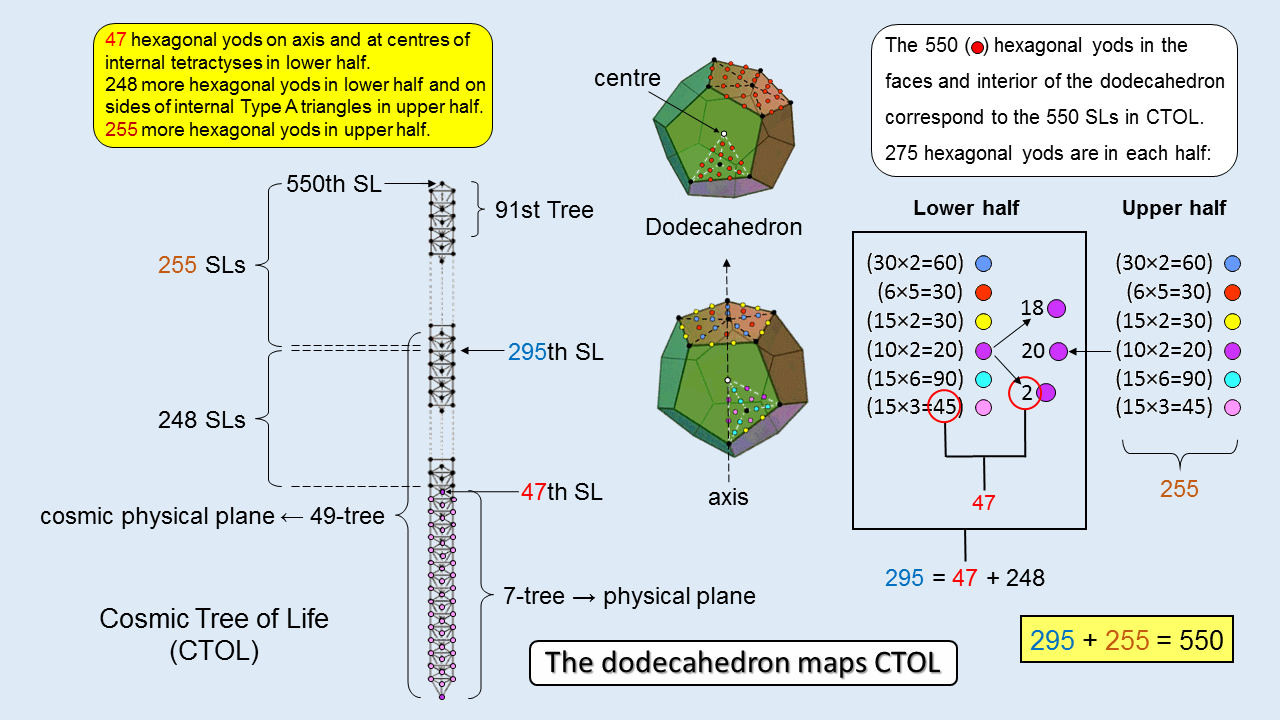
Remarkably, we see that the complete set of 550 hexagonal yod contains subsets that differentiate between the 47 SLs of the 7-tree mapping the physical plane, the next 248 SLs up to Chesed of the 49th Tree and the remaining 255 SLs of CTOL. The 47 hexagonal yods either line the axis or are at centres of tetractyses that formally correspond to Malkuth. In the same way, the physical plane corresponds to Malkuth, being the lowest of the seven planes that correspond formally to the seven Sephiroth of Construction. The 295 SLs up to Chesed of the 49th Tree correspond to the 295 hexagonal yods that are either in the lower half of the dodecahedron or on sides of internal Type A triangles that join vertices in its upper half to its centre. The 255 SLs spanning the 42 Trees that map the six cosmic superphysical planes correspond to the 255 other hexagonal yods in its upper half.

What emerges from the analysis on this page, the previous page and the next page is the existence of a profound and beautiful property of the five Platonic solids that mathematicians have not known about because: 

1. they do not know how to recognize real sacred geometry, even supposing that some of them, perhaps being Platonists, might accept that the concept of 'sacred geometry' is legitimate;
2. they have had little insight into the power and significance of Pythagoras' tetractys as the template of sacred geometries that reveals how they embody numbers of universal (and, therefore, scientific) significance. Mathematicians have understood that, as the representation of the fourth triangular number, the tetractys symbolises the numbers 1, 2, 3 & 4. But their understanding extends little further than that;
3. they have, of course, been unaware of the mathematical map of reality that the author calls "CTOL";
4. they have not realised how various objects that religions traditionally regarded as 'sacred geometry' have properties that, although overtly different, are characterized by the same set of parameters, such as the number 550. Such characterisation is inevitable, given that sacred geometries must be analogous, or isomorphic, being merely alternative versions of the same, universal blueprint. However, mathematicians have never recognised this fact. Instead, they have assumed that no mathematical equivalence or isomorphism underlies sacred geometries because their atheism or agnosticism made them presuppose that no religious geometry can have any significance beyond that of being a symbolic representation of religious beliefs, let alone any connection to science.

The five Platonic solids are the regular polyhedral representation of CTOL. Its 550 SLs are symbolized by the 550 hexagonal yods making up the dodecahedron; they have their geometrical counterpart in the 550 corners, sides & triangles that make up the faces of the five Platonic solids. The icosahedron does not possess this property, despite being the dual of the dodecahedron (see the table). This is because it is one of the four Platonic solids associated with the four "Elements" of the physical universe. The ancient association of the dodecahedron with the celestial sphere has a more profound rationale than the superficial one known to historians of science, i.e., its approximate resemblance to a sphere, although it is true that, for the ancient mind, the sky, or celestial sphere, represented Heaven, the realm of the gods. We now see that the dodecahedron is, truly, the regular polyhedral representation of all levels of reality, both physical and superphysical. But it takes its construction from the tetractys — the template of sacred geometry — to reveal this profound and beautiful property, as well as the Decad — the number that the tetractys symbolizes — to express it arithmetically. Only this particular Platonic solid embodies through its hexagonal yods the number that measures the geometrical composition of the faces of all five Platonic solids, as well as the the number of SLs in the Cosmic Tree of Life. It is, therefore, fitting that the ancient Greeks should have associated it with the fifth Element Aether as the source of the material universe, the particles of whose Elements they believed had the shape of the other four Platonic solids that can be fitted within the dodecahedron.

<< Previous    1  [2]  3    Next >>

Home