#51 The Tetrad  determines the numbers of vertices & edges of the 4₂₁ polytope representing the 240 roots of the exceptional Lie group E₈

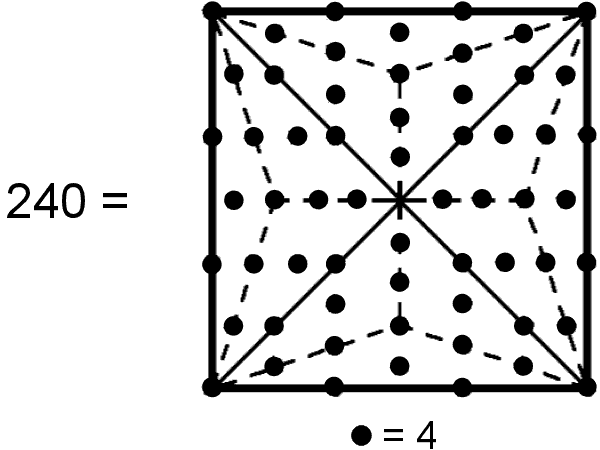
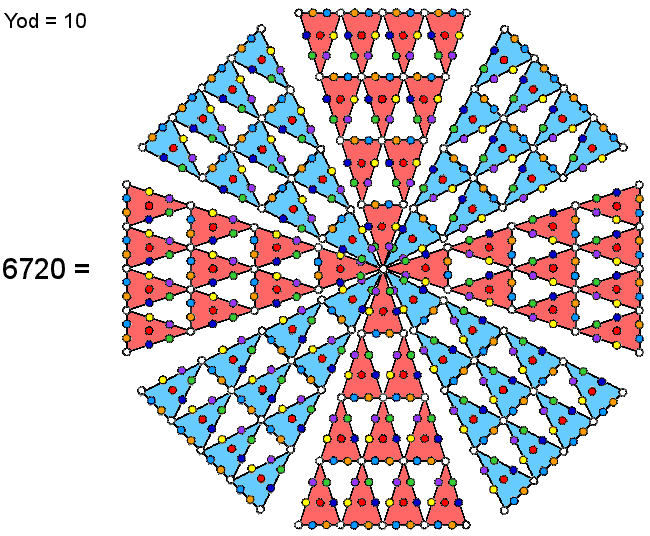
The 60 yods surrounding the centre of a Type B square generate the number 240 when weighted with the Tetrad. This is the number of vertices of the 421 polytope.

An 8-fold array of 2nd-order tetractyses sharing one corner has 672 yods surrounding its centre. Weighted with the number 10 (the 4th triangular number), they generate the number 6720, which is the number of edges of the 421 polytope. Each cross-shaped array of four 2nd-order tetractyses contains 336 yods that represent the 3360 edges of each half of the 421 polytope when the Decad (10) is assigned to each yod.

The square is the simplest, geometrical symbol of the Tetrad. The Type B square had 61 yods. Weighted with the number 4, the 60 yods surrounding its centre generates the number 240, where

240 = (1+2+3+4)×1×2×3×4.

This is the number of vertices of the 4₂₁ polytope whose 8-dimensional position vectors are the root vectors of E₈, the largest of the five exceptional Lie groups.

The 2nd-order tetractys has 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³.

84 yods surround its centre, where

84 = 4¹ + 4² + 4³ = 1² + 3² + 5² + 7².

There are also 84 yods below its apex. Eight 2nd-order tetractyses arranged around their shared apices contain (8×84=672) yods. Weighted with the Decad, they generate the number 6720. This is the number of edges of the 4₂₁ polytope. Each cross-shaped array of four red or four blue 2nd-order tetractyses generates the number (3360) of edges in half this polytope. As the Decad is the fourth triangular number (namely, the 1st-order tetractys), the Tetrad determines the number of vertices and the number of edges of the 4₂₁ polytope. In this way, the number at the heart of the number mysticism of the ancient Pythagoreans determines the very geometrical object whose vertices represent the symmetry group E₈ describing the forces between E₈×E₈ heterotic superstrings. How right the ancient Pythagoreans were for valuing the Tetrad and tetractys so much!

672 yods are needed to construct the first four Platonic solids (tetrahedron, octahedron, cube & icosahedron) from tetractyses (see here & here). This means that they embody the number 6720 when the Decad is assigned to all these yods as their building blocks. Remarkably, the number 1680 paranormally obtained by C.W. Leadbeater when he counted and checked 135 times the number of turns in each helical whorl of the UPA is, simply, the number generated by assigning the Decad to the average number of yods in the four Platonic solids believed by the ancient Greeks to be the shapes of the particles of the four physical Elements Fire, Air, Earth & Water. 672 extra yods are needed to transform into tetractyses all the sectors of the 42 triangles surrounding the centre of the Sri Yantra (see here). It means that they, too, embody the number 6720 when the Decad is assigned to them (see the home page). We saw in #50 how the inner form of 10 overlapping Trees of Life embodies this number. The 4₂₁ polytope conforms to the archetypal pattern of sacred geometries. The implication of this is clear: E₈×E₈ heterotic superstrings exist and were paranormally described by Annie Besant and C.W. Leadbeater.

The number 6720 is related to the superstring structural parameter 16800 and to the dimension 248 of E₈ by:

6720 = 16800×2480/(2²+3²+4²+...+26²),

where 26 is both the gematria number value of YAHWEH and the number of dimensions of the space-time of bosonic strings. As 16800 = 50×336, where

336 = (1²+2²+3²+...+31²)/31,

and 2480 = 80×31,

so that

6720 = 4×10×100×(1²+2²+...+31²)/(2²+3²+4²+...+ 26²) = 4×(1+2+3+4)(1³+2³+3³+4³)(1²+2²+...+31  ²)/(2²+3²+4²+...+26²),

where 26 is the sum of the numbers of combinations of 10 objects arranged in the four rows of a tetractys:

26 = (2¹ − 1) + (2² − 1) + (2³ − 1) + (2⁴ − 1) = 1 + 3 + 7 + 15.*

This shows how the Tetrad expresses the number of edges of the 4₂₁ polytope.

* There are ⁿC_r combinations of r objects taken from a set of n objects, where ⁿC_r = n!/r!(n−r)!. The sum of the numbers of combinations of n objects taken one, two, ... n at a time = 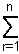 ⁿC_r = 2ⁿ − 1, using the binomial theorem:

(1 + x)ⁿ = 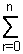 ⁿC_rx^r = 1 +  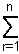 ⁿC_rx^r

and putting x = 1.

<< Previous    1...   49  50  [51]  52  53  ...56    Next >>

Home