| << Previous 1... 4 5 [6] 7 8 ...56 Next >> |
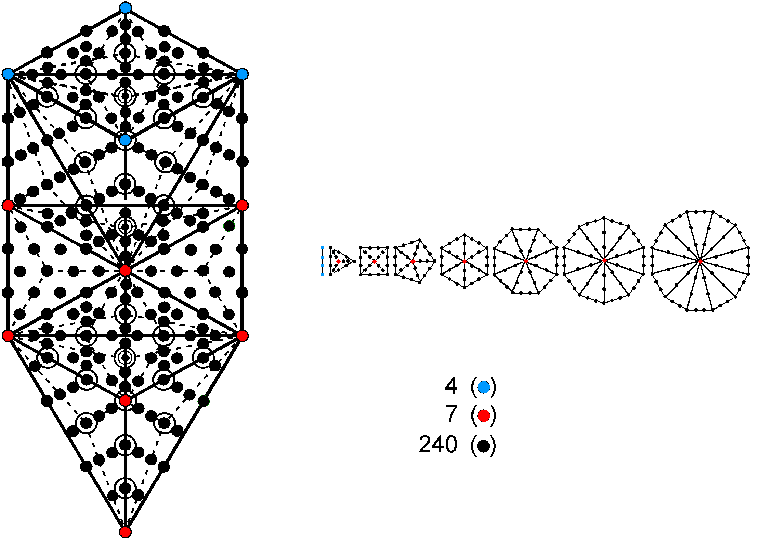
#6 The Tree of Life & the seven separate polygons embody the superstring structural parameter 251

The 1-tree with 19 Type A triangles has 251 yods. They comprise the four blue yods located at Kether, Chokmah,
Binah & Daath, the seven red yods at the positions of the seven Sephiroth of Construction and 240 black yods
created by the conversion of the 19 triangles into Type A triangles (circles in the diagram shown above denote yods
that are directly behind other yods). Consider, next, the root edge and the seven separate regular polygons of the
inner Tree of Life that share this edge. The root edge has four blue yods, and the seven polygons have seven red
centres and 240 black yods that line the sides of their 48 tetractys sectors, making a total
of 251 yods (for the sake of clarity, the hexagonal yods at centres of tetractyses in the polygons are omitted from
the diagram). The Tree of Life parameter 251 is the number of yods needed in both cases to construct from
tetractyses the geometrical shape of both its outer and inner forms. The four yods in the root edge
generating the seven polygons correspond to Kether, Chokmah, Binah & Daath, which stand, so to speak, 'outside'
the planes of being created by the seven Sephiroth of Construction, which correspond to the seven red seed centres
of the polygons making up the inner Tree of Life.
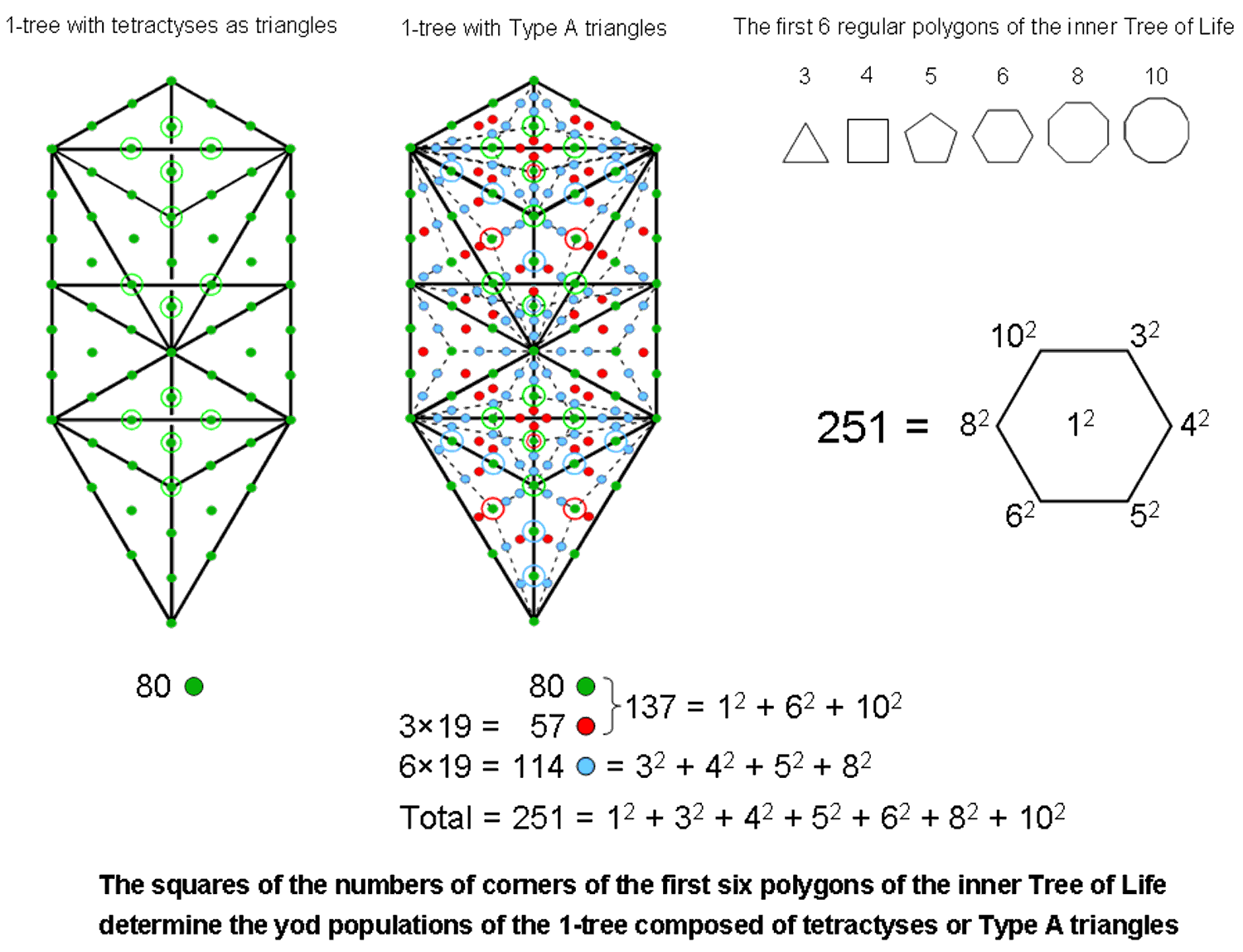
The number 251 has the remarkable property:
251 = 12 + 32 + 42 + 52 + 62 + 82 + 102,
where the integers that are squared are the numbers of corners of the first six separate polygons, "1" denoting one of the ends of the separate root edge. As discussed in #8, the first six polygons enfolded in the 10-tree have 251 corners, showing the equivalence of the 1-tree and the 10-tree. As now shown, certain combinations of these squares determine the numbers of different types of yods in the 1-tree. When its 19 triangles are tetractyses, the 1-tree contains 80 green yods (see below), where 80 is the number value of Yesod, the penultimate Sephirah. Their transformation into Type A triangles adds (3×19=57) red hexagonal yods at the centres of the 57 tetractyses and (6×19=114) blue hexagonal yods on 57 of their (57+25=82) sides, where
114 = 32 + 42 + 52 + 82.
There are (80+57=137) green or red yods, where
137 = 12 + 62 + 102.
This is how the 1-tree embodies the number 137, whose reciprocal is the approximate value of the fine-structure constant α measuring the strength of the coupling to the electromagnetic field of an elementary particle carrying the electric charge of the electron:
Physicists who seek geometrical underpinnings of this famous number should not expect this particular, physical connotation to be explained by the sacred geometry of the 1-tree. What manifests here is yet another example of the character of the number 137 as a defining parameter of any holistic system. The mathematics of quantum electrodynamics incorporates this number because it is part of the still-sought "theory of everything" based upon the divine paradigm that has this number as one of its defining parameters, along with numbers like 26, 248 and 496. It appears explicitly in the first 10 regular Type B polygons enfolded in one another as the 137 corners outside the root edge of their 222 triangles (see next paragraph for the significance of these polygons). Alternatively, there are 137 corners associated with each set of the first 10 polygons that are intrinsic to them in the sense of not coinciding with corners of polygons enfolded in the next higher Tree of Life (see Fig. 15 in Article 58 here).
More evidence for the holistic nature of the number 251 as the yod population of the 1-tree and the number of yods creating the root edge and the 48 sectors of the seven polygons is the following: the three regular polygons absent from this set of polygons are the heptagon with seven corners, the nonagon with nine corners and the undecagon with eleven corners. There are 10 polygons up to the dodecagon. The first six polygons bear a correspondence to the six Sephiroth of Construction above Malkuth, which corresponds to the last polygon, the dodecagon, whilst the three absent polygons correspond to the three members of the Supernal Triad. Assigning the squares of 7, 9 & 11 to the corners of a tetractys, which symbolise the Supernal Triad, and the squares of 3, 4, 5, 6, 8, 10 & 12 to the seven hexagonal yods of this tetractys, with 122 assigned to the central hexagonal yod symbolising Malkuth, their sum is 645:
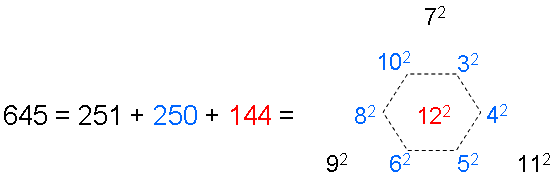
It is remarkable that the sum of the squares of the numbers of corners of the three absent polygons is the holistic parameter 251:
251 = 72 + 92 + 112,
whilst the sum of the squares of the numbers of corners of the first six polygons is 250:
250 = 32 + 42 + 52 + 62 + 82 + 102.
What is the geometrical meaning of the number 645? The 94 sectors of the (7+7) enfolded polygons have 80 corners, where 80 is the number of Yesod. When they are Type B, the polygons have 1370 (=137×10) yods:
|
|
 |
|
|
|
and therefore embody the fine-structure number 137 in a remarkable way, it being the number of tetractyses that have the same number of yods as the inner form of the Tree of Life. The number of yods other than corners = 1370 − 80 = 1290 = 129×10, where 129 is the number value of YAHWEH SABAOTH, the Godname of Netzach (see here). The number of such yods associated* with each set of seven enfolded polygons = 1290/2 = 645. So we see that this number is the number of yods needed to construct each set of seven enfolded Type B polygons from tetractyses, starting from their skeletal division into sectors. Embodied in the first 10 regular polygons as the sum of the squares of their numbers of corners is this very number, whilst the sum of the squares of the numbers of corners of the three polygons absent from the inner Tree of Life is the yod population of its outer form — the 1-tree. This is an amazing property of the inner Tree of Life. The dodecagon has 181 yods, of which 36 yods line its boundary. Hence, (181−36−1=144) yods surround its centre inside its boundary. This is the meaning of the square 122 = 144 at the centre of the tetractys shown above. 144 is the only square Fibonacci number. Moreover, it is the 12th Fibonacci number.
Superstring significance of the Tree of Life parameter 251
In string theory, objects extended in one dimension are called "strings". Quantum mechanics requires space-time to
have 26 dimensions for spinless strings. Imposition of supersymmetry reduces this number to
10. Ten points in 26-d space-time are each located by 25 spatial coordinates, i.e., a total of
10×25 + 1 = 251 space-time coordinates. This is the number of yods in the outer Tree of Life. It is the number of
space-time coordinates of points on the 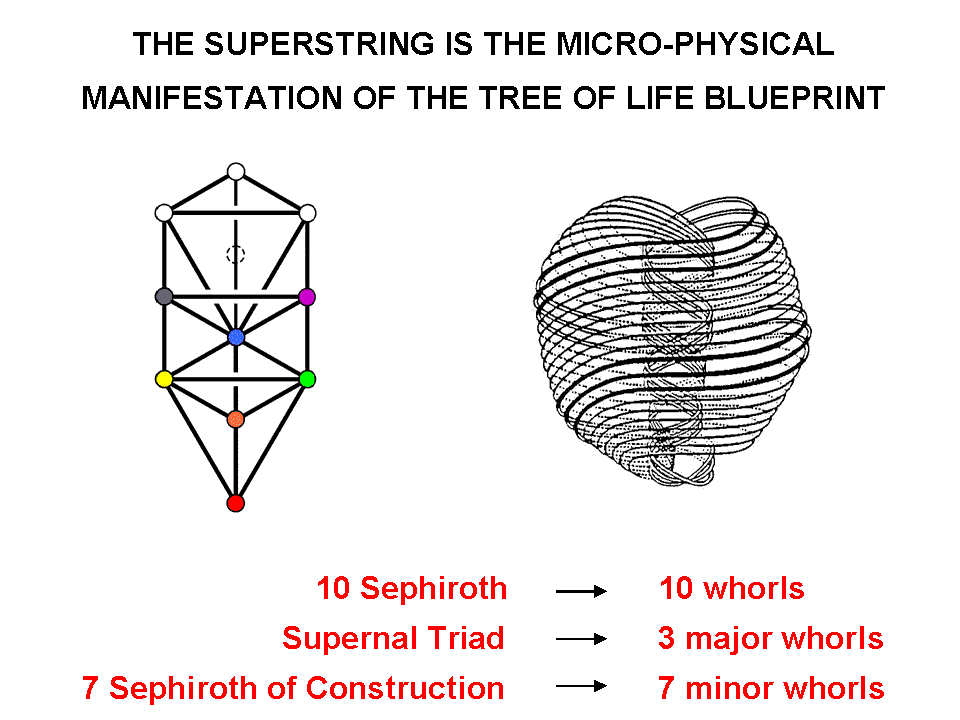 ten closed curves of the UPA, identified by the author as the subquark state of the
E8×E8 heterotic superstring. The yods at Kether, Chokmah, Binah & Daath signify
the coordinates of the three major whorls measured along their lengths (so-called "longitudinal coordinates")
and their common time coordinate. The yods at the seven Sephiroth of Construction denote the longitudinal
coordinates of the seven minor whorls. The 240 other yods symbolize the 24 so-called "transverse coordinates"
of points on each of the 10 whorls, i.e., the coordinates of points measured along the 24 dimensions that are
perpendicular to each whorl at any point along its length. These directions define independent, transverse
modes of vibration of the whorls. The appearance of the number 251 in both the outer and inner forms of the
Tree of Life is therefore consistent with both a prediction of quantum mechanics and the form of the UPA
remote-viewed by Annie Besant & C.W. Leadbeater, once it is realized that the UPA exists in
26-dimensional space-time. However, the two Theosophists described only the 10-dimensional
(superstring) aspect of the object, namely, the 3-dimensional whorl and its six higher orders of spirillae,
which represent the winding of closed curves around the 6-dimensional, compactified space predicted by
superstring theory. Their "bubbles in koilon" are the interface between the space-times of
superstrings and their higher-dimensional structures. According to this view,
E8×E8 heterotic superstrings, which are confined to two 10-dimensional space-time
sheets separated by a narrow gap that extends along the tenth spatial dimension predicted by M-theory, are like
the tips of icebergs. The rest of them extends in 15 higher dimensions of space that was
beyond even the ability of Besant & Leadbeater to explore with micro-psi. Are the topology and symmetries of
this higher space the origin of supersymmetry, false doubts about which have begun to appear amongst some
theoretical physicists owing to the CERN's LHC not detecting squarks (see?
ten closed curves of the UPA, identified by the author as the subquark state of the
E8×E8 heterotic superstring. The yods at Kether, Chokmah, Binah & Daath signify
the coordinates of the three major whorls measured along their lengths (so-called "longitudinal coordinates")
and their common time coordinate. The yods at the seven Sephiroth of Construction denote the longitudinal
coordinates of the seven minor whorls. The 240 other yods symbolize the 24 so-called "transverse coordinates"
of points on each of the 10 whorls, i.e., the coordinates of points measured along the 24 dimensions that are
perpendicular to each whorl at any point along its length. These directions define independent, transverse
modes of vibration of the whorls. The appearance of the number 251 in both the outer and inner forms of the
Tree of Life is therefore consistent with both a prediction of quantum mechanics and the form of the UPA
remote-viewed by Annie Besant & C.W. Leadbeater, once it is realized that the UPA exists in
26-dimensional space-time. However, the two Theosophists described only the 10-dimensional
(superstring) aspect of the object, namely, the 3-dimensional whorl and its six higher orders of spirillae,
which represent the winding of closed curves around the 6-dimensional, compactified space predicted by
superstring theory. Their "bubbles in koilon" are the interface between the space-times of
superstrings and their higher-dimensional structures. According to this view,
E8×E8 heterotic superstrings, which are confined to two 10-dimensional space-time
sheets separated by a narrow gap that extends along the tenth spatial dimension predicted by M-theory, are like
the tips of icebergs. The rest of them extends in 15 higher dimensions of space that was
beyond even the ability of Besant & Leadbeater to explore with micro-psi. Are the topology and symmetries of
this higher space the origin of supersymmetry, false doubts about which have begun to appear amongst some
theoretical physicists owing to the CERN's LHC not detecting squarks (see?
The following correspondences exist between the 251 yods in the 1-tree and the 251 space-time coordinates of points on the 10 whorls of the UPA:
| Daath | → | time coordinate common to each point. |
| 10 Sephiroth | → | 10 longitudinal coordinates of points on the 10 whorls. |
| 240 yods other than Daath & Sephiroth | → | 240 transverse coordinates of points on the 10 whorls |
| 251 yods in the 1-tree | → | 251 coordinates of points on the 10 whorls. |
They exist for the simple reason that the UPA is the Malkuth level of the microscopic realisation of the Tree of Life blueprint, as expressed by the 1-tree, so that each of the 251 yods in the latter denotes a coordinate of a point on each of its string-like whorls, with Daath corresponding to the time coordinate shared by all 10 independent points on the 26-d space-time sheet. Readers should ask themselves: how could such correlations exist unless Annie Besant and C.W. Leadbeater had genuine micro-psi powers that objectively described subatomic particles as manifestations of the geometry of the Tree of Life? This cannot have arisen by chance because, as shown on pages 7 & 8, the same holistic parameter 251 appears both in the inner form of a single Tree of Life and in the inner form of 10 Trees — the full representation of the former — and it is implausible in the extreme that chance could account, too, for these properties.
| << Previous 1... 4 5 [6] 7 8 ...56 Next >> |