Most books and websites devoted to sacred geometry never reveal the true reason why the Platonic solids are an example of "sacred geometry." They refer, of course, to Plato's book Timaeus, his exposition on cosmology, where the Greek philosopher, heavily borrowing from the ideas of Pythagoras, sets out the notion that the particles making up the elements Earth, Water, Air & Fire have the respective shapes of the cube, icosahedron, octahedron & tetrahedron. The Pythagoreans associated the fifth regular polyhedron, the dodecahedron, with the celestial sphere because of the approximation of its shape to that of a sphere. Following the introduction by Aristotle of Aether, the fifth Element, it came to be associated with this Element. These websites also point out how prevalent these shapes are in nature and how the Golden Ratio displayed in their geometry manifests in the proportions of many living things, as though these examples supposedly used by God to create everything were enough to prove their sacred nature! But such things, however beautiful and ubiquitous, do not constitute proof that the Platonic solids possess sacred geometry. No one now believes that atoms themselves take the form of the regular polyhedra, although their aggregation in crystals do, indeed, often show these shapes for reasons that are well understood by chemists and physicists. What determines whether an object has sacred geometry is the possession of the universal, mathematical design or pattern found in the sacred geometries of religions and parameterised by the same set of numbers. This pattern has been explored in depth in the author's new book.

Like any other example of sacred geometry, the real quality of "sacredness" in the Platonic solids is revealed by uncovering the numbers that they embody. Only after they have been extracted and found to be identical to the set of numbers in other sacred geometries can one start to claim that this congruence implies the existence of a universal, mathematical pattern which originates in the Mind of God and, therefore, that the geometry is, indeed, sacred because it encapsulates — as a Platonist would say — the archetypal "Ideas" of God. The numbers that characterize the Platonic solids are the 50 gematria number values of the ten Sephiroth in the four Worlds (see table). As Plato's Ideas originate in the Archetypal World (Atziluth), it is not surprising that the numbers embodied in the ten Divine Names — the essence of the Sephiroth in Atziluth — should make a strong presence in quantifying the properties of such archetypal objects. The most obvious example of this is ELOHIM, the Godname of Binah, which embodies the divine archetypes of "form," or pattern of relationship, at its most basic level of meaning. Its gematria number value is 50, which is both the number of vertices of the five Platonic solids and the number of their faces — the basic geometrical elements that determine their shape in 3-dimensional space. Ways in which all the Godnames mathematically express their properties are discussed at length in Article 3 (WEB, PDF).

There are two ways of transforming straight-line, geometrical objects, having reduced them to triangles:

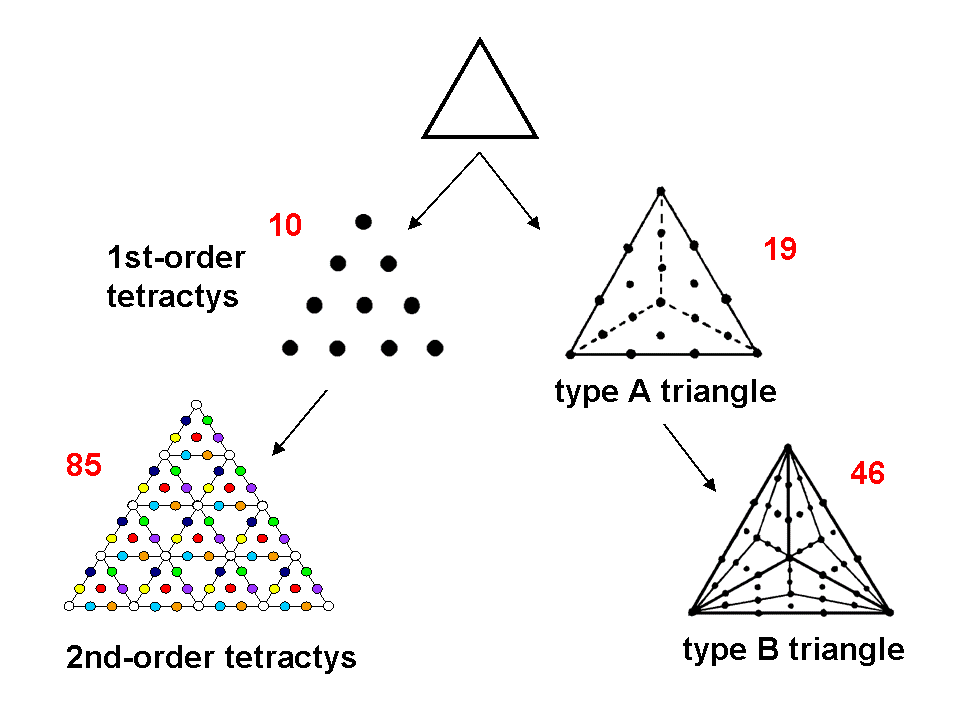
1. turn the triangles into Pythagorean (1st-order) tetractyses, then 2nd-order tetractyses, etc;
2. turn the triangles into type A triangles, type B triangles, etc by dividing them into their three sectors, each sector into three sectors, and so on.

Counting the different classes of yods (corners of tetractyses, hexagonal yods, boundary yods, interior yods, etc) generates a set of numbers that will have their counterparts in other sacred geometries if the object in question possesses sacred geometry. Not only this, if these numbers display certain relationships between them that are found in other sacred geometries as well, this enables the object to be identified as having sacred geometry and therefore embodying numbers of scientific or metaphysical significance. Finally, the properties of such holistic objects will always be mathematically beautiful. Perfection and beauty are the sine qua non of Divine Truth. They are the signature of sacred geometry. This beauty is conceptual, not necessarily aesthetic. It is therefore harder to identify, even with the eye of a mathematician. What is needed is a correctly trained eye. University departments do not offer courses in such training.

In the following pages, the true sacred geometry of the Platonic solids will be partly established by comparing their properties with those of the Tree of Life and then showing that they are analogous. Their correspondence with other sacred geometries is analysed in the section Correspondences.

 

<< Previous    1...   2  3  [4]  5  6  ...19    Next >>

Home