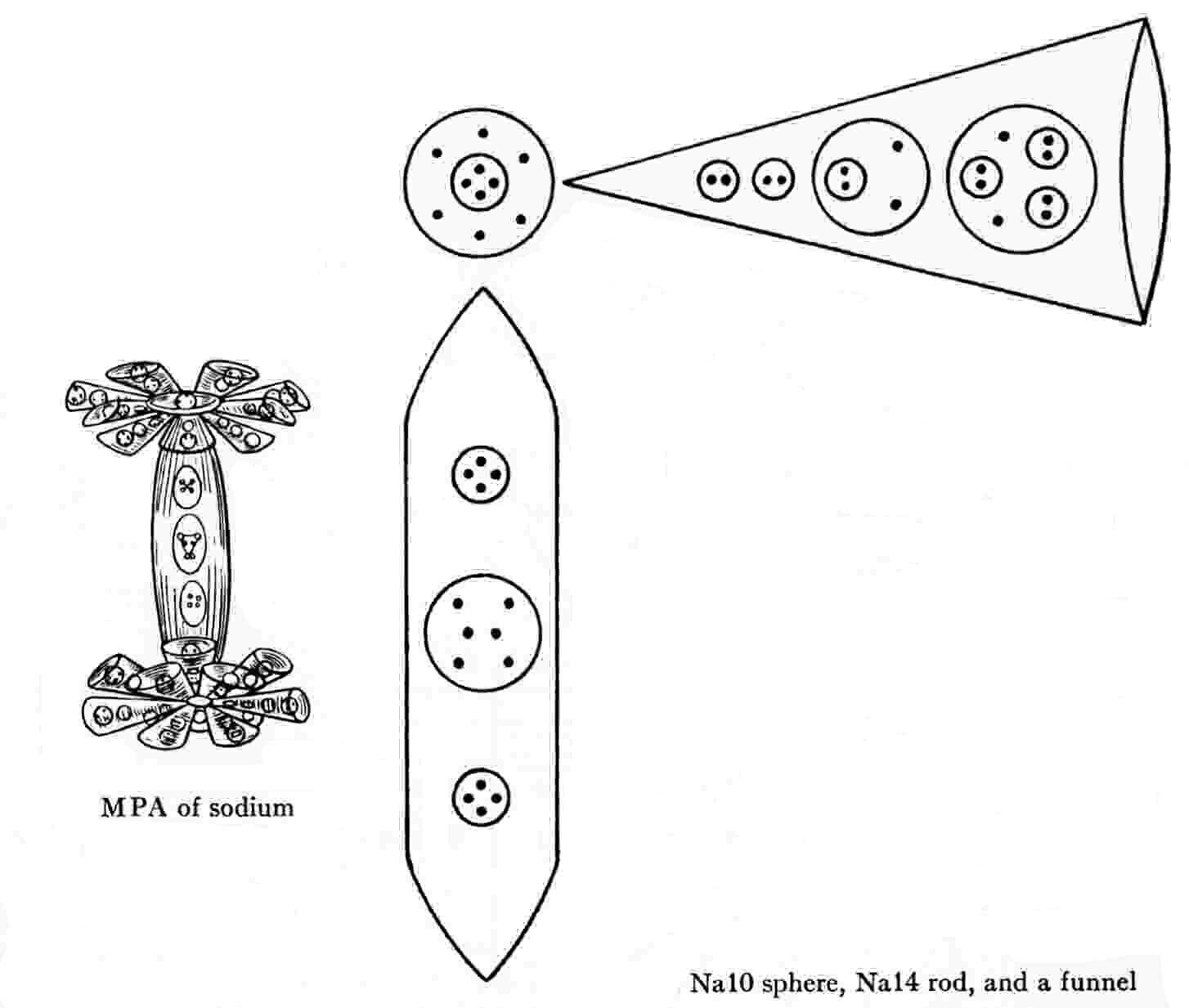
The Sodium MPA
The MPA of sodium is shaped like a dumb-bell. The connecting rod (Na14) of the dumb-bell contains fourteen UPAs arranged in three spheres of four, six and four UPAs. At each end of the rod are two concentric spheres (Na10), the inner one enclosing four UPAs, the outer one containing six UPAs. Twelve funnels radiate symmetrically in the same plane from each pair of spheres. Each funnel (Na16) contains sixteen UPAs arranged in four spheres, two containing pairs of UPAs, one enclosing a pair of pair of UPAs and two
free UPAs and the fourth containing three pairs of UPAs and two free UPAs.
Sodium MPA = Na14 + 2Na10 + 24Na16.
The sodium MPA is formed from two Na23 nuclei, which provide 414 subquarks —
four fewer than the number of UPAs. The 384 subquarks making up sixty-four u quarks and sixty-four d quarks are
distributed equally among the twenty-four funnels. Six of the funnels at one end of the dumb-bell each contains
twelve X subquarks and four Y subquarks; each of the other six funnels contains twelve Y subquarks and four X
subquarks, i.e., six funnels are the mirror states Na16′ of the other six; similarly for the twelve funnels at the
other end of the dumb-bell. The diagram below shows the subquark 
composition of one of the former types of funnel. The fourteen X subquarks and the sixteen Y
subquarks in the remaining four u quarks and six d quarks provided by the two nuclei fill the rod and Na10
globes. The inner sphere in each Na10 should contain a (0) duad (X-Y), not the reported group of four UPAs.
The outer sphere encloses a 3X-3Y bound state. The disintegration diagram confirms this because it shows that
the group of six UPAs in a globe breaks up at the E2 stage into a (+) triplet (u quark) and a (−) triplet (d
quark):
3X-3Y → u (=2X-Y) + d (=X-2Y).
The Na14 contains a 2X-4Y bound state and two 2X-2Y bound states. The disintegration diagram confirms this by indicating that the former breaks up at stage E2 into a (−) duad (Y-Y) and two (0) duads (X-Y):
2X-4Y → Y-Y + 2(X-Y),
and that the latter breaks up into four (0) duads (X-Y):
2(2X-2Y) → 4(X-Y).
The Na16 group in twelve funnels comprises:
1. a X-X and a Y-Y bound state (as indicated by the (+) and (−) duads labelled "a");
2. a bound state of two X subquarks and two free X subquarks (as shown by the (+) quartet labelled "b", which breaks up into two (+) duads (X-X));
3. in c another bound state of two X subquarks and two free X subquarks, which recombine into a (+) quartet (4X) that splits up at stage E2 into two (+) duads (X-X),as well as two X-Y bound states, which link up and then divide again at stage E2 into two (0) duads (X-Y).
The discrepancy between the 418 UPAs counted in the MPA and the predicted 414 subquarks is due to a predicted mal-observation of the particle in the inner sphere of each Na10 globe, namely, the quartet of UPAs in each globe should have been a (0) duad. Apart from this, every type of particle is consistent with the hypothesis that the sodium MPA was formed from two Na23 nuclei.
