How the ancient Hebrew Godnames prescribe the general Tetrahedral Lambda

A. 2-dimensional  lattice of musical number weights.	B. The general Tetrahedral Lambda. The colour of the text identifying each face is that of its edges.

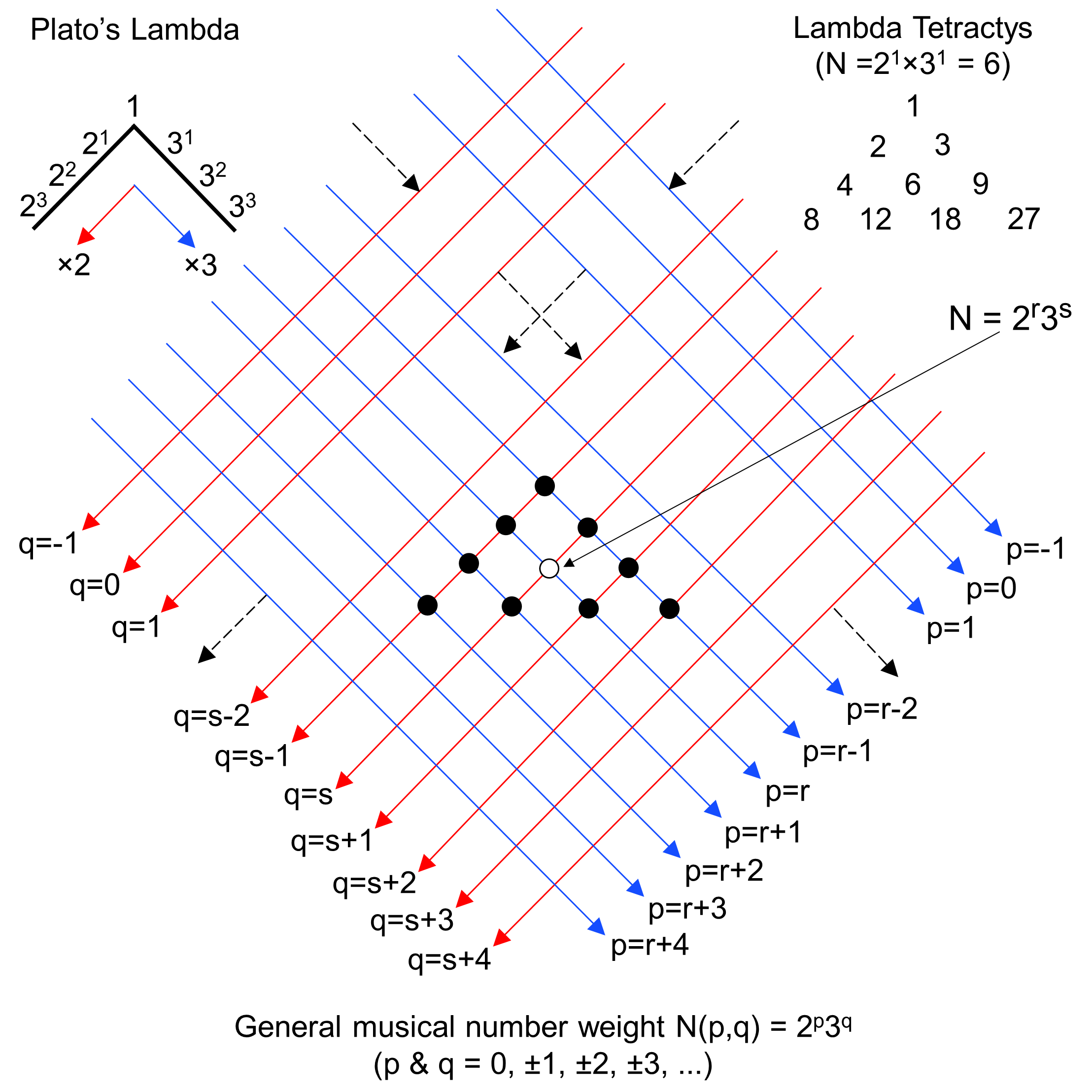
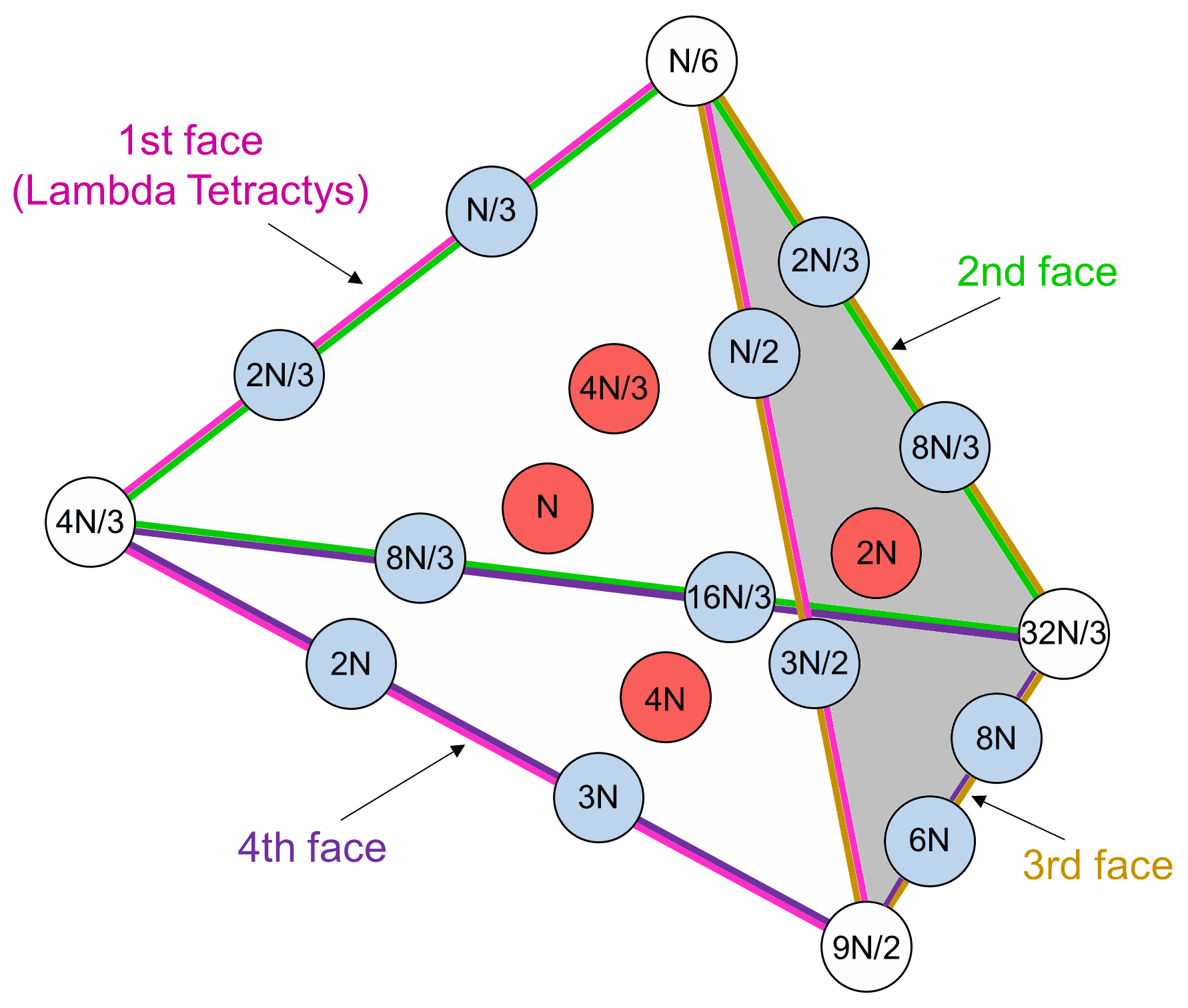
We have seen that Plato's Lambda is but two sides of a tetractys array of 10 musical number weights that the author calls the "Lambda Tetractys." This, in turn, is but the first face of a tetrahedral array of 20 musical number weights that the author calls the "Tetrahedral Lambda." The number weights in the first face are just a set of 10 numbers in the shape of a tetractys with the integer 1 at its apex that can be selected from an infinite lattice of such numbers. They form rows of numbers that extend to infinity in both directions parallel to each side of the tetractys (see image A shown above). If the tetractys is equilateral, this 2-dimensional lattice is hexagonal, each number being surrounded by six nearest neighbours at the corners of a hexagon. A number weight is of the form 2^p3^q (p = 0, ±1, ±2, ±3, etc; q = 0, ±1, ±2, ±3, etc). A number weight 2ⁿ3^m is located at the intersection of the line p = n and the line q = m, e.g., the number weight 1 is the intersection of the line p = 0 containing the first four powers of 3 that form one slope of Plato's Lambda and the line q = 0 that contains the first four powers of 2 forming its other slope. The lines p = 1 and q = 1 intersect at the centre of the Lambda Tetractys, where the number weight 6 is located. If the tetractys is shifted so that its new centre is the number weight N = 2ⁿ3^m located at the intersection of the lines p = n and q  = m, its new apex is located at the intersection of lines p = n − 1 and q = m − 1, i.e., the number weight 2ⁿ⁻¹3^m−1 = N/6. This means that every weight in the new tetractys gets multiplied by N and divided by 6. Apart from that, the numbers in the new tetractys bear the same relative proportions to one another. The sum of its 10 number weights is 15N. Every number in the Tetrahedral Lambda is similarly changed. The sum of the 20 new weights in the generalised Tetrahedral Lambda (see image B) is 175N/3. The numbers at its four vertices are N/6, 4N/3, 9N/2 & 32N/3; their sum is 50N/3. The sum of the 16 weights not at vertices = 175N/3 − 50N/3 = 125N/3. The weights at the centres of its four faces are N, 4N/3, 2N & 4N; their sum is 25N/3. The sum of the 16 weights on the six edges is 175N/3 − 25N/3 = 50N.

Elsewhere on this website, it was shown that the Tetrahedral Lambda extrapolated from the Lambda Tetractys is isomorphic to the inner Tree of Life in the sense that the sum (350) of its 20 number weights is equal to the number of hexagonal yods lining all the sides of the 94 tetractyses in the (7+7) enfolded polygons. This and correspondences with other sacred geometries demonstrated elsewhere indicate its archetypal character as the arithmetic counterpart of the general holistic pattern embodied in sacred geometries. As such, the Godnames of the 10 Sephiroth arithmetically prescribe its properties. However, the presence of their gematria number values is hidden within these properties when they are quantified. They are more clearly revealed by considering the generalised Tetrahedral Lambda instead of that generated by a specific Tetrahedral Lambda whose apex is the number 1. It must be emphasized that — just as with the generalised Lambda Tetracys —  we are dealing with the same tetrahedral array of number weights except that each weight is multiplied by the same factor of N/6. A Godname number may appear as a factor not only as itself but in a factor that is twice itself because a Godname whose gematria number value is n can prescribe the nth even integer as well as the nth integer. This means that any combination of weights whose sum is of the form 2nN, nN, nN/3 (2nN/6) or nN/6 counts as a prescription by a Godname (as all number weights in the Tetrahedral Lambda have been divided by 6, which has only the factors 2 and 3, no other denominators appear). As with many other examples discussed elsewhere, numbers of the form 10n, where n is a Godname number, must also be regarded as being prescribed by this Godname. The ways in which the ancient Hebrew Godnames prescribe properties of the general Tetrahedral Lambda are shown below, starting with the first Sephirah and ending with the last Sephirah:

Kether: EHYEH = 21
Sum of the weights at the four vertices and the three smallest weights at centres of faces = 50N/3 + N + 4N/3 + 2N = 21N. Sum of weights at corners and centre of 1st face = N/6 + 4N/3 + 9N/2 + N = 42N/6 = 2×21N/6 (= 7N). Sum of the four weights on the 3rd sloping edge = N/6 + 2N/3 + 8N/3 + 32N/3 = 85N/6. Sum of the 12 weights on the five other edges = 50N − 85N/6 = 215N/6. Excluding the two basic weights N/3 & N/2 (see the discussion for Netzach for definition of "basic weight"), the sum of the 10 remaining weights = 215N/6 − N/3 − N/2 = 210N/6 = 10×21N/6 (= 35N).

Chokmah: YAH = 15 & YAHWEH = 26
Sum of the 10 weights in the 1st face = 15N. Notice that the two weights on the base of the Lambda Tetractys interpolated from the seven weights forming the lambda add up to 5N and the remaining eight weights add up to 10N, thereby reproduicing the letter value 5 of he (ה) and the letter value 10 of yod (י) in the Divine Name יה. The sum of the 10 other weights in the 2nd, 3rd & 4th faces = 175N/3 − 15N = 130N/3 = 10×26N/6.

Binah: ELOHIM = 50
Sum of the weights at the four vertices = 50N/3 (see above). Sum of the 16 weights on edges = 50N (see above). Sum of the weights at the centres of the 4 faces = 25N/3 = 50N/6.

Chesed: EL = 31
Sum of the seven weights in the 4th face that are either at its centre or at the corners of a hexagon = 2N + 8N/3 + 16N/3 + 8N + 6N + 3N + 4N = 31N.

Geburah: ELOHA = 36
Sum of the 10 weights in the 1st face = 15N. The central weight is N. Sum of the nine weights on the three edges of the 1st face = 14N. Sum of the 16 weights on the six edges = 50N (see above). Sum of the seven weights on the three edges outside the 1st face = 50N − 14N = 36N.

Tiphareth: YAHWEH ELOHIM = 76
Sum of the six weights on the three edges outside the 1st face other than the largest weight 32N/3 = 36N − 32N/3 = 76N/3.

Netzach: YAHWEH SABAOTH = 26 + 103 = 129
The weight 2N/3 on the third sloping edge of the general Tetrahedral Lambda is the counterpart of the weight 4 for the case when N = 6. This weight is analogous to the weights 2 & 3 in the Lambda Tetractys whose counterparts in the general case are N/3 and N/2. These three basic weights generate all the other weights. Sum of the seven weights below the apex weight N/6 on the three sloping edges that are not these basic weights =

N/6 + 2N/3 + 4N/3 + 3N/2 + 9N/2 + 8N/3 + 32N/3 = (N/6 + 3N/2 + 8N/3) + (2N/3 + 4N/3 + 9N/2 + 32N/3)

  = 26N/6 + 103N/6 = 129N/6.

Notice that the weights add up separately to 26N/6 and 103N/6, where 26 is the number value of YAHWEH and 103 is the number value of SABAOTH.

Hod: ELOHIM SABAOTH = 50 + 103 = 153
Sum of the largest central weight 4N and the seven weights on the three sloping edges other than the three basic weights
= 26N/6 + 4N + 103N/6 = 50N/6 + 103N/6 = 153N/6.
Notice that the weights add up separately to 50N/6 and 103N/6, where 50 is the number value of ELOHIM and 103 is the number value of SABAOTH.

Yesod: EL CHAI = 49
The weight N/6 at the apex, the weight N/3 and the weight N/2 are the counterparts of the basic integers 1, 2 & 3 that generate all the 10 number weights of the Lambda Tetractys. Their sum is N. The 16 weights lining the six edges add up to 50N. Sum of the 13 other weights on edges generated by the counterparts of these three basic weights = 50N − N = 49N.

Malkuth: ADONAI = 65
Sum of the four weights lining the base of the general Lambda Tetractys = 4N/3 + 2N + 3N + 9N/2 = 65N/6. Sum of the 10 weights above the 4th face = N/6 + N/3 + N/2 + 2N/3 + 2N/3 + N + 3N/2 + 2N + 8N/3 + 4N/3 = 65N/6. Notice that rearrangement of these numbers generate the values of the four letters alef (א), dalet (ﬢ), nun (נ) & yod (י) of ADONAI:

ADONAI→ADNI = 1 + 4 + 50 + 10 = 65:

N/6 + 2N/3 + (N/2+2N/3+N+3N/2+2N+8N/3) + (N/3+4N/3) = (1+4+50+10)N/6 = 65N/6.

General comment
It is particularly impressive evidence of the Godnames at work that the sum of the 16 weights lining the edges of the general Tetrahedral Lambda is 50N. This is because, as the Godname of Binah, the source of all archetypes governing the form of a holistic system, ELOHIM with number value 50* prescribes the sum of the 16 weights that delineate the shape of the Tetrahedral Lambda because they form the edges of the tetrahedron defined by its four vertices. It is clear, indisputable evidence of how ELOHIM prescribes the archetypal pattern of the Tetrahedral Lambda in a manner that conforms to the metaphysical meaning of Binah as Logos, the universal divine reason that transforms the amorphous, creative chaos of Chokmah into order and organisation. The various sums that have been discussed here are of the form nN, nN/6 & 10nN/6, where N is the weight at the centre of the 1st face and N/6 is the weight at the apex of the general Tetrahedral Lambda. When N = 6, i.e., when the 1st face is the Lambda Tetractys, the sum of these 16 weights is 300, which is 50×6, whilst the sum of the weights at the vertices is 100, which is the 50th even integer, and the sum of the weights at centres of faces is 50. The sum of the 10 weights outside the 1st face = 260 = 26×10, demonstrating how YAHWEH prescribes the Tetrahedral Lambda. The sum of the weights at the centres of the three faces outside the Lambda Tetractys = 50 − 6 = 44, so that the sum of the seven weights outside the Lambda Tetractys that line edges = 260 − 44 = 216 = 6³ = 6×6×6. The centre of the 1st face, the sum of the weights at its vertices and the sum of the weights lining edges outside it are, respectively, 6¹, 6² and 6³. The number 36 (= 6²) is the number value of ELOHA, the Godname assigned to Geburah, the sixth Sephirah of Construction, and the number 216 (= 6³) is the number value of its Hebrew name. It is the sum of the same integer 6 assigned to each of the 36 yods surrounding the centre of a Type A hexagon, the six-sided regular polygon. A Type B hexagon has 90 yods surrounding its centre. This is the sum of the 10 weights in the 1st face (see Fig. 13 on page 8). The Type A→Type B change adds 54 yods; this is the sum of the seven number weights creating the lambda shape of the Lambda Tetractys (also the sum of the seven weights not at the corners of the 1st face). So the Type A hexagon is the counterpart of the weights at the three corners of the Lambda Tetractys and the Type B hexagon is the counterpart of the whole Lambda Tetractys. Surrounding the centre of the Type C n-gon are 42n yods. There are 252 yods surrounding the centre of the Type C hexagon; this is the sum of the 10 weights on the three edges of the Tetrahedral Lambda outside its 1st face that meet at the number weight 64, which is the largest of the 20 number weights in the Tetrahedral Lambda. The first three types of hexagon therefore embody parameters that shape it. They do not appear as random combinations of weights but, rather, as those weights that progressively determine its two-dimensional and three-dimensional shapes according to the sequence:

* Here is remarkable evidence that the gematria number value of ELOHIM is 50, not 86, as normally calculated by Kabbalists, who fail to realise that the value 40 of the letter M (mem) must be contracted to 4 when it part of this word. It is, of course, not obvious that this step should be necessary, and it is convincing evidence, repeated in many sections of this website, that demonstrates that it is correct. If it were not, the display in the general Tetrahedral Lambda of the three other Godname numbers (76, 129 & 153) that incorporate this amendment would have to arise by chance, and this is a highly implausible scenario.

Home