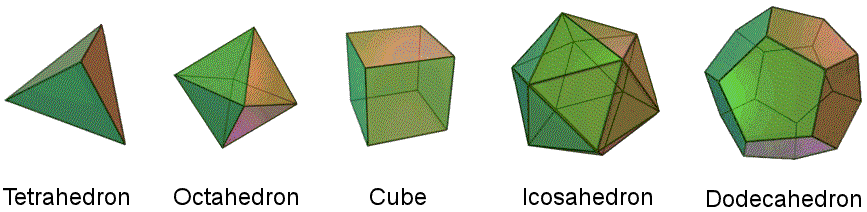
Figure 10. The 5 Platonic solids.
| << Previous 1... 5 6 [7] 8 9 ...16 Next >> |
The Lambda Tetractys pattern in the five Platonic solids and the disdyakis triacontahedron
 |
Figure 10. The 5 Platonic solids. |
The five Platonic solids (Fig. 10) have the following numbers of edges:
|
tetrahedron |
octahedron |
cube |
icosahedron |
dodecahedron |
Total |
|
6 |
12 |
12 |
30 |
30 |
90 |
The tetrahedron and the dodecahedron (or icosahedron) have 36 edges and the octahedron, cube & icosahedron (or dodecahedron) have 54 edges. This is the polyhedral manifestation of the fundamental 36:54 division of holistic systems, as expressed in the first face of the Tetrahedral Lambda:
| 1 |
1 |
||||||||||||||||||
| 2 | 3 | 2 | 3 | ||||||||||||||||
| 4 | 6 | 9 |
= |
+ |
4 |
6 |
9 |
= |
36 + 54. |
||||||||||
| 8 | 12 | 18 | 27 | 8 | 27 | 12 | 18 |
This face embodies the holistic parameter 90, which manifests as the 90 edges of the five Platonic solids that shape the mathematically complete set of the regular, 3-dimensional polyhedra.
The same division appears in the disdyakis triacontahedron, discussed here. Its 180 edges are the sides of 180 triangles inside it that share the centre of the polyhedron as a vertex. They have (180×3=540=54×10) sectors. Its 120 triangular faces have (120×3=360=36×10) sectors. The polyhedron contains (360+540=900=90×10) triangles. The 36:54 division differentiates its exterior from its interior!
|
|
|
The number of yods in an n-gon (n-cornered polygon) whose sectors are Type A triangles = 15n + 1, where "1" denotes its centre. Sixty vertices of the disdyakis triacontahedron surround an axis that passes through two diametrically opposite vertices. When the latter are A, B & C vertices, these 60 vertices are corners of, respectively, seven, 11 & 15 n-gons. In each case, (15×60=900) yods surround their centres (Fig. 11) when their sectors are Type A triangles. They comprise 60 red yods at the outer corners of the 60 sectors, 480 blue hexagonal yods on the internal sides of the tetractyses and 360 black yods on the sides & centres of sectors. Apart from the tetractys factor of 10, this is the 6:48:36 pattern of the first face of the Lambda Tetrahedron. It demonstrates that the disdyakis triacontahedron conforms to the archetypal pattern of integers in the Lambda Tetractys.
The Tetrad Principle formulated in Article 1 expresses the characteristic properties of holistic systems. Here are examples of this principle at work:
900 = 302 = (3+6+9+12)2 = (12+22+32+42)2,
360 = 4×900/10 = (22+42+62+82)2/(1+2+3+4),
60 = 22 + 23 + 24 + 25,
480 = 8×60 = 23(22+23+24+25) = 25 + 26 + 27 + 28,
and
(360+480=840) = 84×10 = (12+32+52+72)(1+2+3+4).
The numbers 900, 360, 60, 480 & 840 are expressed by the sums of the first four integers or their squares, four consecutive powers of 2, the sums of the squares of the first four even/odd integers or products of these sums.
| << Previous 1... 5 6 [7] 8 9 ...16 Next >> |