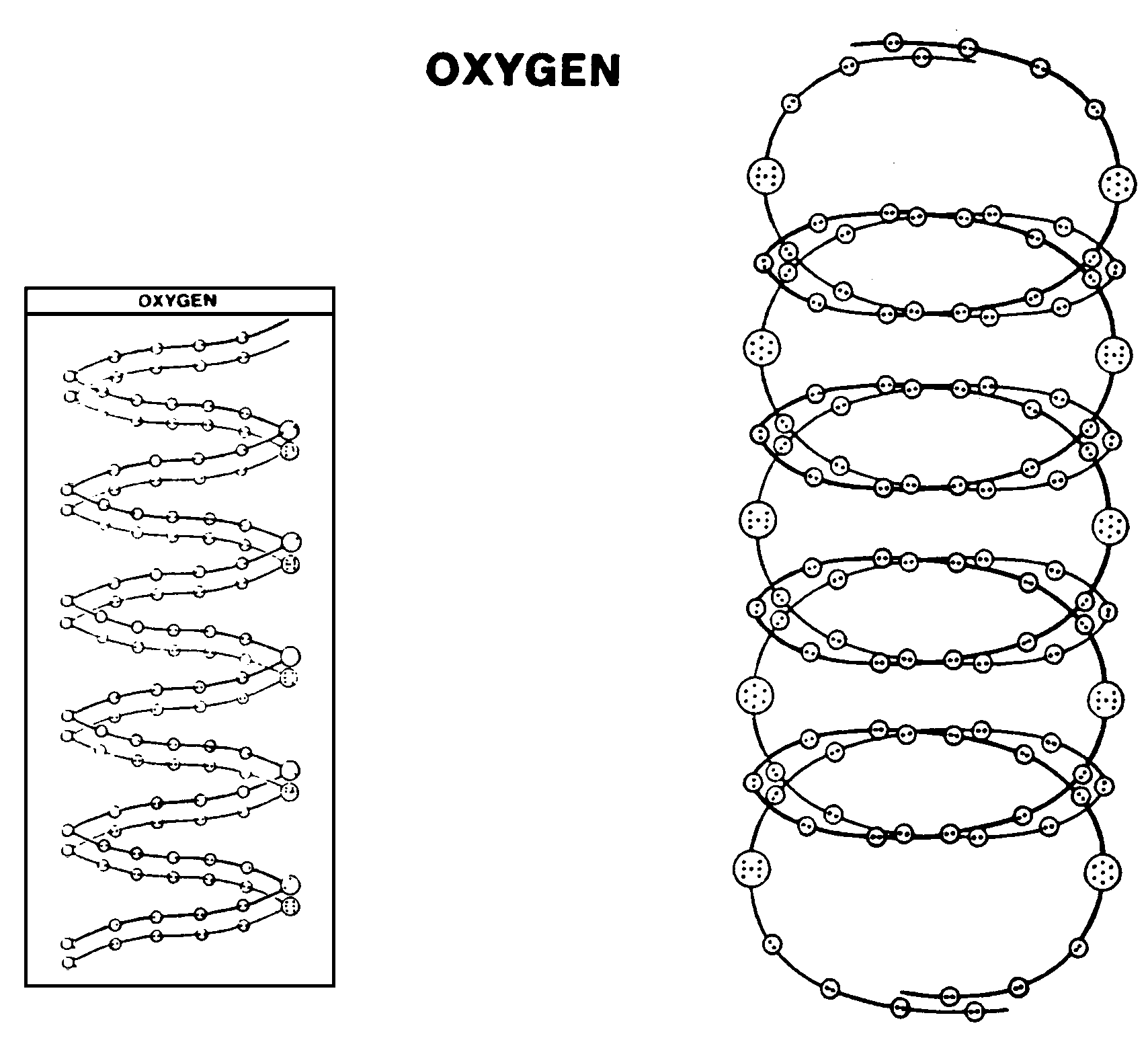
The Oxygen MPA

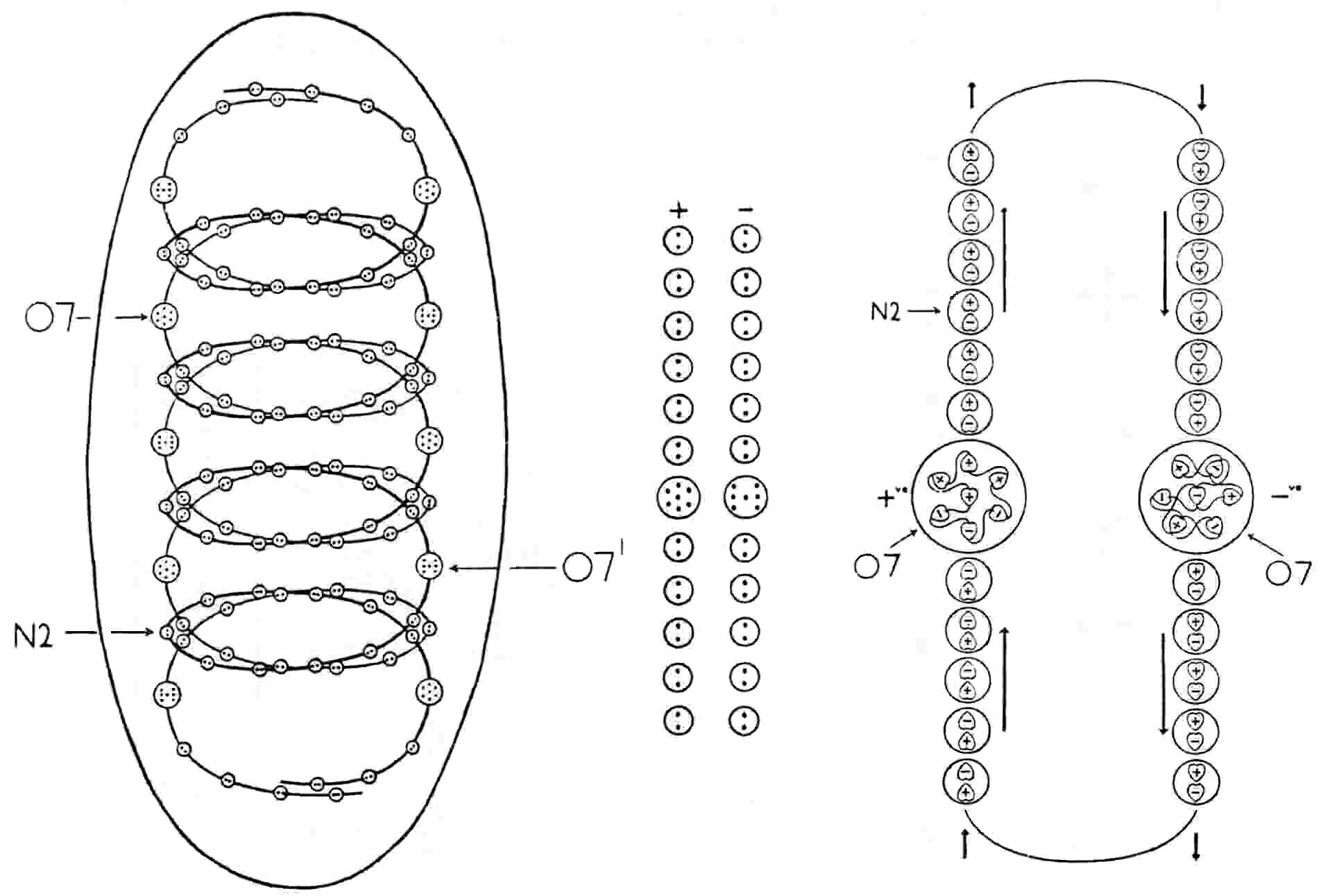
The form of the oxygen MPA is unlike that of any other element. It is ovoid and encloses two spirally-coiled bodies, one 'positive,' the other 'negative,' revolving rapidly in opposite directions about a common axis parallel to their length. Each spiral body is a chain of fifty-five much smaller spheres containing two UPAs (N2), one (+) and the other (−). Each body is shaped like a spring with five coils and has a brilliantly lit point shining on each coil. This point is actually a globe containing seven UPAs. The major difference between the two spirals is in their central globes. In the positive spiral, denoted (+), the globes (called 'O₇') contain a central (+) UPA surrounded by a face-centred cubic array of six UPA, three (+) and three (−). In the negative spiral, denoted (−), the globes (called 'O₇′') contain a central (−) UPA, about which are arranged three (+) UPAs and three (−) UPAs, two being perpendicular to each other and inclined to the third pair, which lies on a line with the central UPA. The two spirals spin around their shared axis so fast as to present to micro-psi vision a continuous surface, creating the appearance of a solid cylinder.

Oxygen MPA = (55N2 + 5O₇) + (55N2 + 5O₇′)

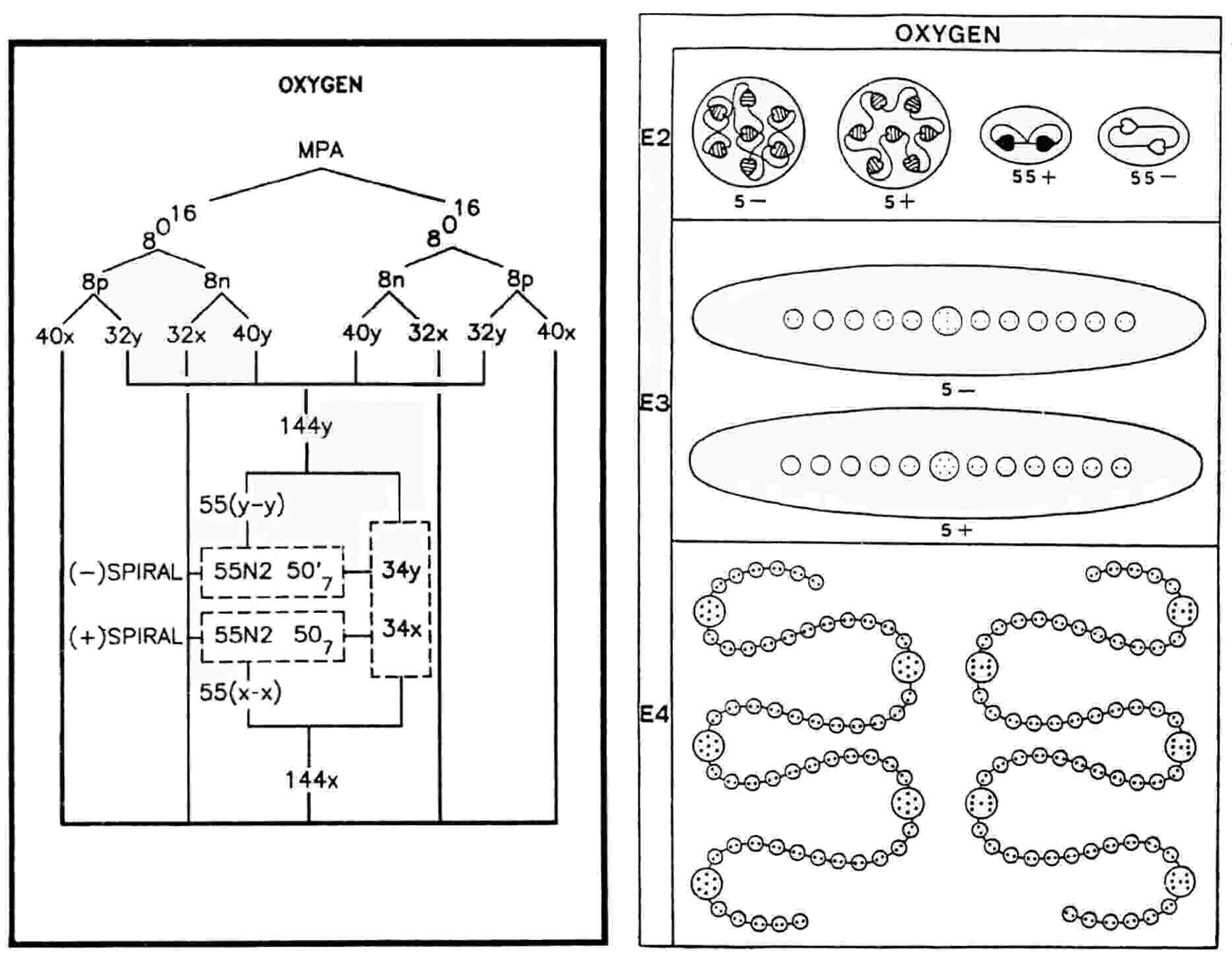The oxygen MPA is formed from two O¹⁶ nuclei, which contain forty-eight u quarks and forty-eight d quarks. No reason can yet be given for why micro-psi examination of an oxygen molecule should disintegrate its two O¹⁶ nuclei into two chains of particles that are bound states of two subquarks behaving like dipoles aligned end-to-end and interdispersed by groups of seven subquarks bound together by strings. The two nuclei provide 288 subquarks, that is, two less than the number of UPAs. Because the MPA consists of two halves of similar form, this symmetry makes it more plausible that one too many UPAs was observed in both halves than that one half had two fewer UPAs than the other. It also seems more probable that one too many UPAs was observed in one of the O₇ and in one of the O₇′ than that one of the N2 in each spiral body was actually a single UPA that went unnoticed. Furthermore, it is likely that these were a (+) and a (−) UPA because the MPA would then contain 144 (+) UPAs and 144 (−) UPAs, which would be consistent with it having been formed from two oxygen nuclei with thirty nucleons, a pair of nucleons having, according to the interpretation of the hydrogen MPA, nine (+) and nine (−) UPAs:

MPA = 144 (+) + 144 (−) = 16[9(+) + 9(−)].

The O₇ and O₇′ groups predicted to have one fewer UPAs will be called, respectively, 'O₆' and 'O₆′'.

Each of the fifty-five N2 groups in the (+) spiral is an X-X bound state; each N2 in the (−) spiral is a Y-Y bound state. This is confirmed by the disintegration diagram, which shows that the MPA releases at the E2 stage fifty-five (+) duads (X-X) and fifty-five (−) duads (Y-Y). Thirty-four X subquarks and thirty-four Y subquarks make up the two sets of five globes. The subquark composition of each globe cannot be deduced from the diagram because they were not broken up into their constituents. Two facts, however, allow it to be deduced:

1. The O₇ was called positive and the O₇′ was called negative. In keeping with the general result that the positivity and negativity of bound states of UPAs refer to the sign of their electric charge, if a positively charged O₇ has n X subquarks, each of charge +5/9, and (7−n) Y subquarks, each of charge −4/9, then its total charge is

(1/9)[5n − 4(7−n)] > 0,

i.e., 9n>28. Therefore, n>4. The facts that the same numbers of X and Y subquarks make up all the globes and that each spiral contains the same number of globes means that each negatively charged O₇′ is the mirror state of O₇, containing n Y subquarks and (7-n) X subquarks. Its total charge is

(1/9)[5(7−n) −4n] < 0,

i.e., 9n>35. Therefore, n>4. An O₇ (O₇′) with five, six or seven X (Y) subquarks and, respectively, two, one or no Y (X) subquarks is positively (negatively) charged;

2. The disintegration diagram of the oxygen MPA published in the first edition of Occult Chemistry differs from that above published in the third edition by indicating that the (−) O₇′ group released at the E2 stage consists (looking from top to bottom) of a (−) duad (Y-Y), a (−) linear hydrogen triplet H3′ (d quark = X-2Y) and a second (−) duad (Y-Y), i.e., the O₇′ is made up of one X and six Y subquarks, so that n = 6. This agrees with the second of its three possible configurations deduced above to have a net negative charge.

In order to be consistent with both the first edition disintegration diagram and their polarities assigned by Besant & Leadbeater, the O₇ must be a 6X-Y bound state and its mirror state — the O₇′ — must be an X-6Y bound state. The O₆ should consist of either six X subquarks or five X subquarks and one Y subquark, whilst the O₆′ must consist, respectively, of either six Y subquarks or five Y subquarks and one X subquark (either one X is absent from an O₇ and one X from an O₇′). Remarkably, the total subquark composition of these groups implied by their observed polarities and by the disintegration diagram of the first edition of Occult Chemistry agrees precisely with the thirty-four X and thirty-four Y subquarks required by theory because:

4O₇ + 4O₇′ + O₆ + O₆’ = 4(6X-Y) + 4(X-6Y) + (6X or 5X-Y) + (6Y or X-5Y) = 34X + 34Y.

This is convincing evidence of the correctness of the theory that MPAs are formed from pairs of atomic nuclei.

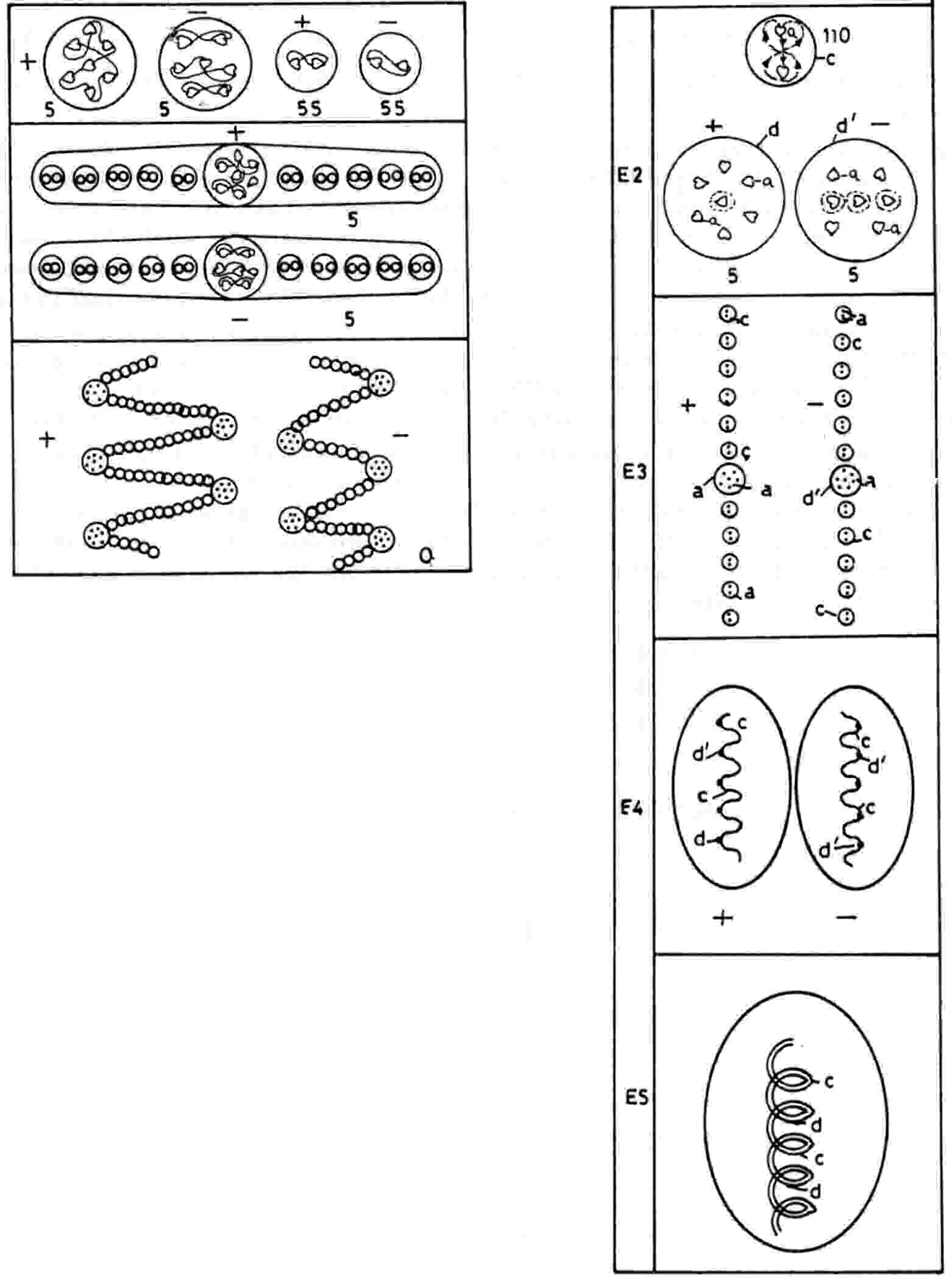The oxygen MPA is an example of small differences to be found occasionally between the disintegration diagrams of MPAs published in the first and third editions of Occult Chemistry. These "edition variants" are relatively few but highly important as tests of any theory of MPAs because both compositions of the MPA implied by these diagrams have to be compatible with this theory. In 1895, Besant published in the Theosophical magazine Lucifer descriptions of the MPAs of hydrogen, nitrogen and oxygen. According to the disintegration diagram she gave there for oxygen, the two spirals broke up at the E2 stage into 110 duads of UPAs pointing in the same direction, that is, (0) duads. Making the plausible assumption that the O₇ and O₇′ groups have the same compositions in the earlier and later versions of the oxygen MPA, the subquark composition of the 110 (0) duads must be the same as that of 55 (+) duads and 55 (−) duads. This means that the subquarks in two (0) duads consist of those in one (+) duad and one (−) duad. A priori, the u and d quarks making up protons and neutrons in atomic nuclei could comprise up to six differently charged subquark species q_r (r = 1-6). Labeling the three recorded types of duads:

(+) = q_i − q_j

(−) = q_k − q_l                     (i, j, k, l, m, n = 1-6)

(0) = q_m − q_n,

then

q_i − q_j + q_k − q_l = 2(q_m − q_n).

Either:

Case A
q_i = q_j = q_m (or q_n) ≡ X

and

q_k = q_i = q_n (or q_m) ≡ Y,

or:

Case B
q_i = q_k (or q_l) = q_m (or q_n)

and

q_j = q_l (or q_k) = q_n (or q_m).

But the trivial case B must be wrong because it implies — contrary to observation — that the (+), (−) and (0) duads must have electric charges of the same sign as they consist of the same types of subquarks. Therefore, only case A is permitted and the two edition variants of the oxygen MPA imply that

 (+) = X-X,
(−) = Y-Y,
 (0) = X-Y.

As the (+) duad is positively charged and the (−) duad is negatively charged, it may be inferred that X carries a positive charge and that Y carries a negative charge. The fundamental interpretation of these types of duads used for the analysis of MPAs — far from being arbitrary — can actually be inferred from the two edition variants of oxygen and the natural interpretation of Besant's and Leadbeater's terms "positive" and "negative" as referring to electric polarity. This refutes the criticism that the interpretation of duads is model-dependent. Instead, it can be deduced from a self-consistent analysis of the observations!

Home