The Fluorine MPA
The fluorine MPA.
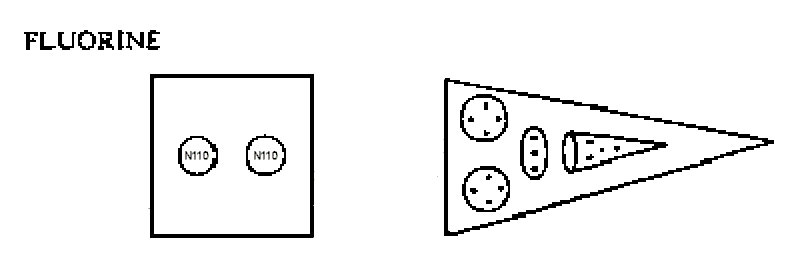
The MPA of fluorine has a cylindrical body containing two N110 spheres and eight spikes, or reversed funnels, each of which contains three quartets of UPAs (two Be4 groups and one Li4 group) and a linear hydrogen triplet (H3′) similar to that present in one of the hydrogen triangles of the hydrogen MPA.
Fluorine MPA = 2N110 + 8(2Be4 + H3′ + Li4).
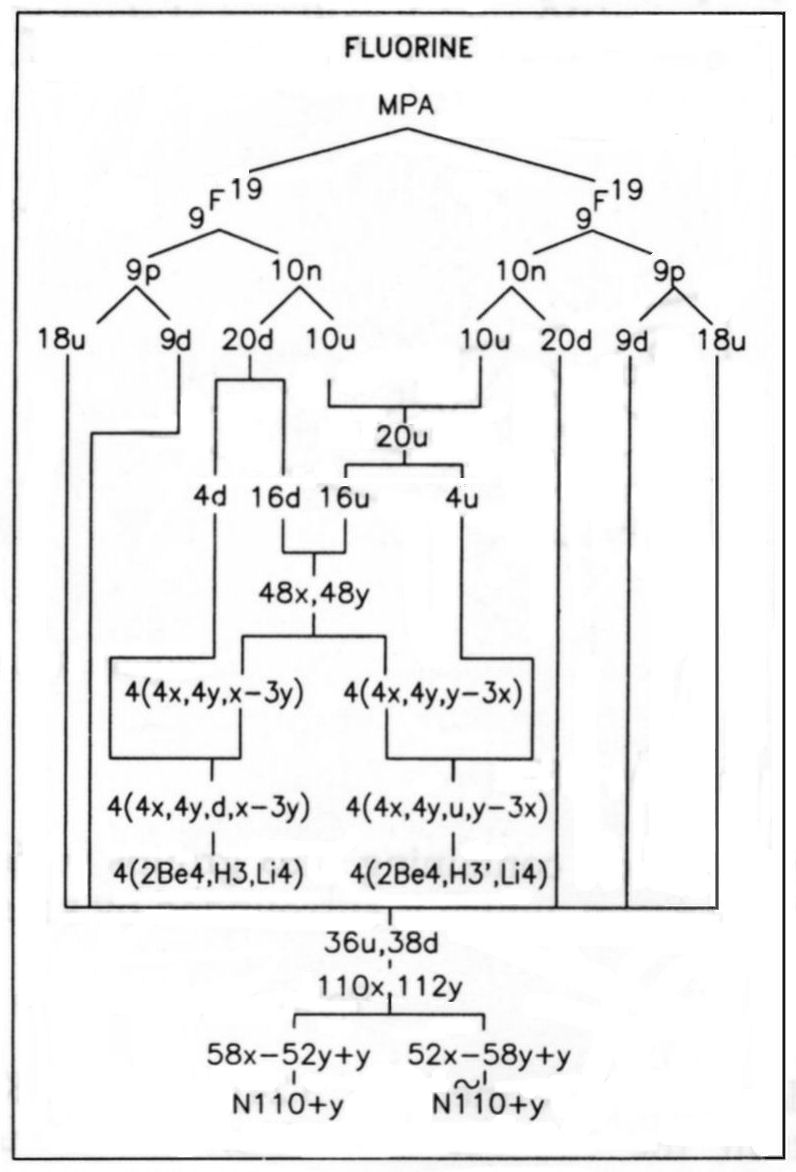The MPA is formed from two F19 nuclei, which provide 342 subquarks — two more
than the number of UPAs. One N110 group contains fifty-eight X subquarks and fifty-two Y subquarks (the same
as that found for this group in the analysis of the nitrogen MPA); the other N110 is the mirror state N110′,
containing fifty-eight Y subquarks and fifty-two X subquarks. The reason why the two N110 groups cannot have
the same composition is that, if they were, the spikes would consist of fifty-four X subquarks and sixty-six Y
subquarks, neither of which numbers is divisible exactly by either 8 or 4, which means that neither X nor
Y subquarks could be distributed equally among either eight or four spikes. This is possible only if one N110
group is the mirror state of the other. One extra Y subquark should be in each N110, accounting for the two
additional subquarks that should be in the MPA. The eight-fold array of spikes prohibits two of them being
different in composition from the other six. The possibility that the same type of group in different MPAs
could differ slightly in their UPA population was anticipated by Besant & Leadbeater, who remarked: "In
the heavier elements, such as gold, with 3,546 Anu, it would be impossible to count each Anu without quite
unnecessary waste of time, when making a preliminary investigation. Later, it may be worth while to count each
division separately, as in some we noticed that two groups, at first alike, differed by 1 or 2
Anu."1
Four spikes contain particles which are the mirror states of their counterparts in the other four spikes. Four spikes each contain a 3X-Y bound state (Li4), a u quark (H3′), a bound state of four X subquarks (Be4) and a bound state of four Y subquarks, the mirror state Be4′ of the Be4 group, The other four spikes each contain an X-3Y bound state, the mirror state Li4′ of the Li4 group, a d quark (H3′), a bound state of four X subquarks (Be4) and a bound state of four Y subquarks, the mirror state Be4′ of the Be4. The diagram below displays the identified UPAs in these predicted two types of spikes.
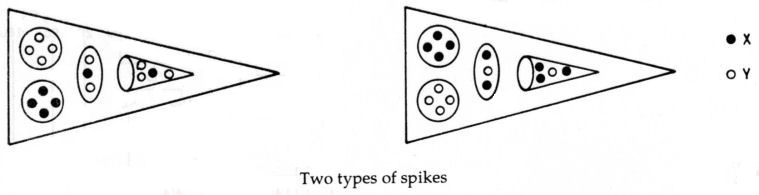
Below is shown the disintegration diagram for the MPA. It confirms the identification of particles for the former set of spikes because it shows a spike having a (+) triplet (u quark), a (+) Be4 group (4X), which breaks up into two (+) duads (X-X), a (−) Be4 group (4Y), which splits up at stage E2 into two (−) duads (Y-Y), and an Li4 group which breaks up into a (+) duad (X-X) and a (0) duad (X-Y), in agreement with its identification as a 3X-Y bound state:
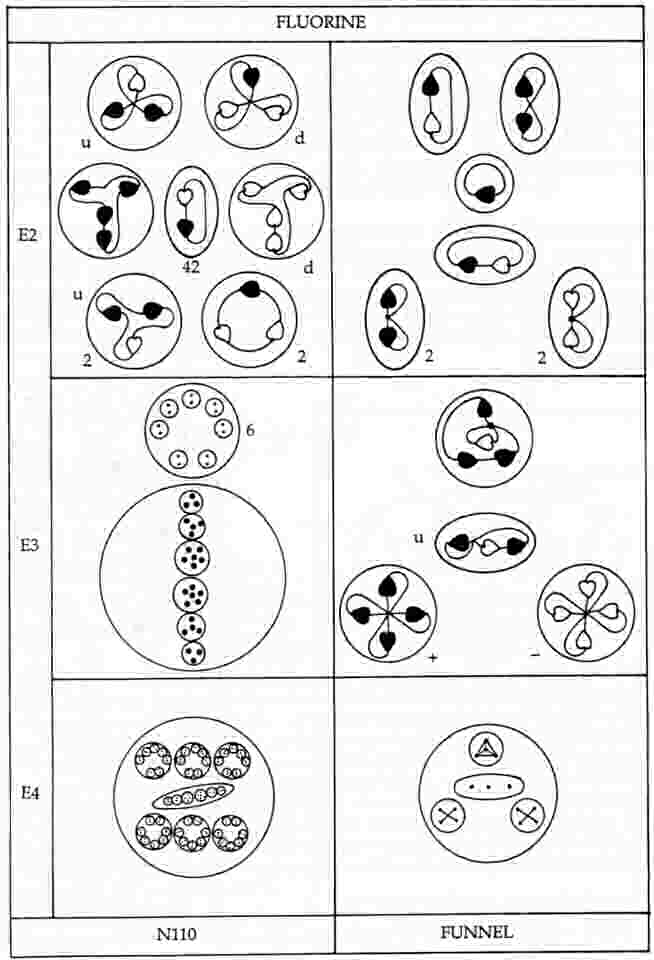
3X-Y → X-X + X-Y.
It is not yet clear why the fluorine MPA displays eight spikes (rather than, say, six or seven). To this extent, the explanation of the fluorine MPA given here is incomplete. But its incompleteness is no excuse for ignoring the remarkable degree of agreement between the author's theoretical identification of particles and the description by Besant & Leadbeater of what they saw when they used micro-psi to examine fluorine. It is, of course, far too detailed and exact to be due to coincidence. It should be enough for the reader to marvel at the degree of correlation between theory and observation, for this does not depend on the details of the factors determining how MPAs are shaped. All it requires are facts about atomic nuclei and the well-established quark model of their protons and neutrons. Even the compositions: (+) duad = X-X, (−) duad = Y-Y and (0) duad = X-Y do not amount to additional hypotheses, for the analysis of the oxygen MPA proved that they can be deduced by demanding consistency between the particles described in the first and third editions of Occult Chemistry.
References
1. Occult Chemistry (3rd ed.), p. 30.
