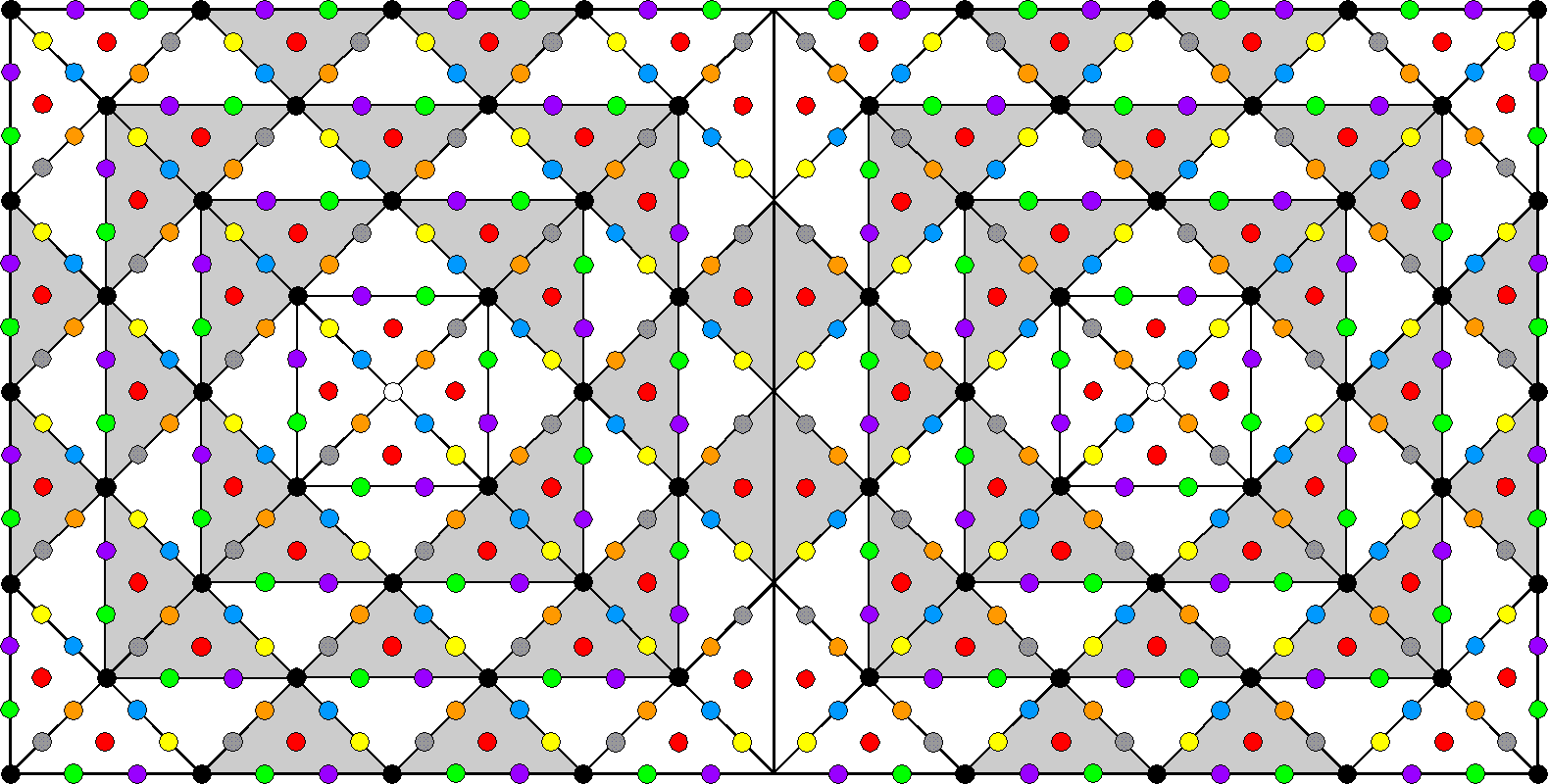
550 yods outside their root edge surround the centres of two joined squares with 2nd-order tetractyses as their sectors.
| << Previous 1... 11 12 [13] 14 15 Next >> |
Representation of CTOL parameter 550 by two joined squares
 |
|
550 yods outside their root edge surround the centres of two joined squares with 2nd-order tetractyses as their sectors. |
A 2nd-order tetractys contains 85 yods, where
85 = 40 + 41 + 42 + 43.
13 yods line each side, so that (85−13=72) yods are added by each sector of an n-gon when it is a 2nd-order tetractys. The number of yods in an n-gon constructed from 2nd-order tetractyses ≡ N(n) = 72n + 1, where "1" denotes its centre. The number of corners of 1st-order tetractyses = 10n + 1 and the number of hexagonal yods = 62n. Notice that 72 is the number of Chesed and that 62 is the number of Tzadkiel, the Archangel of this Sephirah. For the square (n=4), the number of yods surrounding its centre is
N(4) = 4×72 = 288 = 11 + 22 + 33 + 44 = 1!×2!×3!×4!.
They comprise 40 corners (35 outside one side) and 248 hexagonal yods (240 outside one side), where 248 is the number of Raziel, the Archangel of Chokmah. For two joined squares, (288−13=275) yods outside their shared root edge surround the centre of each square. Symbol of the Tetrad, the square determines the number of SLs in CTOL because (275×2=550) yods outside their root edge surround the centres of two joined squares. They comprise (35+35=70) black corners of (40+40=80) 1st-order tetractyses and (240+240=480) coloured hexagonal yods, each square having 240 hexagonal yods outside the shared side. Hence, the two separate squares contain (248+248=496) hexagonal yods. This is the square representation of the (248+248=496) roots of E8×E8, one of the two symmetry groups known to describe superstring forces that are free of quantum anomalies. The two sets of eight hexagonal yods that line two sides of the separate squares that become the root edge of the joined squares symbolise the two sets of eight simple roots of E8×E8. We discover that the square provides a natural connection between the number (550) of Sephirothic emanations in CTOL and the root composition of E8×E8. The Tetrad determines all properties of the pair of squares. For example, it determines their 70 corners outside the root edge because 70 is the fourth, 4-dimensional, tetrahedral number* after 1, whilst 35 (number of corners of 1st-order tetractyses in each square outside the root edge) is the fourth tetrahedral number after 1. It determines their 80 2nd-order tetractyses because 80 = 10×8, where 10 = 1 + 2 + 3 + 4 and 8 = 4th even integer. It determines their 480 hexagonal yods because
480 = 16×30 = 42×(12+22+32+42) = 42 + 82 + 122 + 162.
It determines their 550 yods outside the root edge that surround their centres because 550 = 10×55, where 10 = 1 + 2 + 3 + 4 and 55 is the fourth, square pyramidal number** after 1. Including its centre, each square has 36 corners of 40 1st-order tetractyses outside the root edge, where 36 = sum of the first four odd integers and the first four even integers:
36 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = (1+3+5+7) + (2+4+6+8).
* A tetrahedral number is the number of points in a tetrahedral stack of triangular arrays of
points; a 4-dimensional, tetrahedral number is the number of points needed to construct the 4-dimensional version
of a tetrahedron, called the "pentachoron," "4-simplex" or "5-cell" (see here).
** A square pyramidal number is the number of points in a stack of square arrays of points that form a pyramid.
| << Previous 1... 11 12 [13] 14 15 Next >> |