ARTICLE 52

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
A systematic analysis of the angles subtended by pairs of simple roots of all Lie groups is carried out. The number value 21 of EHYEH, the Godname of Kether, is the number of pairs of orthogonal roots of E8 and the number of angles between the seven simple roots of E7, its largest exceptional subgroup. The number value 15 of YAH, the older version of YAHWEH, the Godname of Chokmah, is the number of pairs of orthogonal roots of E7 and the number of angles between the six simple roots of E6, which is the next largest exceptional subgroup of E8. None of the exceptional Lie groups has a dimension that is a Godname number. Allowing dimensions of groups to be 10×Godname number, the Godname numbers 21, 15 & 36 define dimensions of subgroups of E8. Only 21 & 15 define groups of less rank than E8, all of which are its subgroups. Only 21 & 15 define groups of rank less than or equal to that of E8 whose numbers of orthogonal pairs of simple roots are Godname numbers. The letter values of EHYEH & YAH denote the numbers of right angles between sets of simple root vectors of E6, E7 & E8. The integers 1-15 forming a cross pattée array sum to 4960. This is the number of space-time components of the 496 gauge fields of E8×E8 & SO(32), which are the gauge symmetry groups of the heterotic superstring. A cross pattée array of integers 2-26 add up to 24800, showing how YAHWEH determines the dimension 248 of E8. The Godnames ELOHIM, EL, YAHWEH SABAOTH & ELOHIM SABAOTH also determine this number. ELOHIM with number value 50 prescribes 496 because this number is the arithmetic mean of the first 50 triangular numbers after 3.
1
Table 1. Number values of the ten Sephiroth in the four Worlds.
1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living Creatures)
833Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50Tzaphkiel
(Contemplation of God)
311Aralim
(Thrones)
282Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216ELOHA
(The Almighty)
36Samael
(Severity of God)
131Seraphim
(Fiery Serpents)
630Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101Malachim
(Kings)
140Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148YAHWEH SABAOTH
(Lord of Hosts)
129Haniel
(Grace of God)
97Tarshishim or Elohim
1260Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15ELOHIM SABAOTH
(God of Hosts)
153Raphael
(Divine Physician)
311Beni Elohim
(Sons of God)
112Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246Cherubim
(The Strong)
272Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351Cholem Yesodoth
The Breaker of the Foundations.
The Elements.
(Earth)
168
(All numbers in this table referred to in the article are written in boldface).
2
1. Numbers of EHYEH & YAH prescribe E8
The gematria number values of the ancient Hebrew Godnames have hitherto been found to prescribe the dimensions of the Lie groups E8 and E8×E8 or SO(32) either arithmetically or in the geometrical context of the yod population of overlapping trees or the yod/corner populations of enfolded polygons generated by the Tree of Life. In this article, we shall demonstrate how the Godname numbers of Kether and Chokmah select E8 and its two exceptional subgroups E7 and E6 from the infinite number of Lie groups. Because of its importance in proving rigorously that Godnames prescribe superstring physics, the following discussion must be technical. It is therefore intended primarily for mathematicians and physicists. For this reason, readers unfamiliar with group theory are advised to turn to the simplified summary on page 10.
The mathematician E. Cartan showed in 1894 that there are four* infinite series of simple Lie algebras:
Dn, generates SO2n An, generates SUn+1
n = 1, 2, 3, 4
Cn, generates Sp2n Bn, generates SO2n+2
and five "exceptional" Lie algebras:
The structure of a simple Lie algebra or group G is defined completely by a set of (rank G)-dimensional vectors called "simple roots," which span the "root space" of G, a (rank G)-dimensional Euclidean space. The "Dynkin diagram" specifies the set of simple roots αi (i = 1, 2, 3... rank G) of G. Each simple root is denoted by a dot in 2-d space. In the case of a G having αi's with two different lengths |αi|, the longer roots are denoted by open dots " š " and the shorter roots by filled-in dots "●" (no simple group has roots with three or more different lengths). There are four possible angles θij between any pair of simple roots αi and αj in root space:
150° 90°
135° 120°
The angle between a pair of simple roots is denoted in the Dynkin diagram of G by lines connecting corresponding dots. The following convention is used:
* This is an example of the Tetrad Principle discussed in Article 1.
3
Shown below is an exhaustive list of the Dynkin diagrams of all simple Lie algebras G: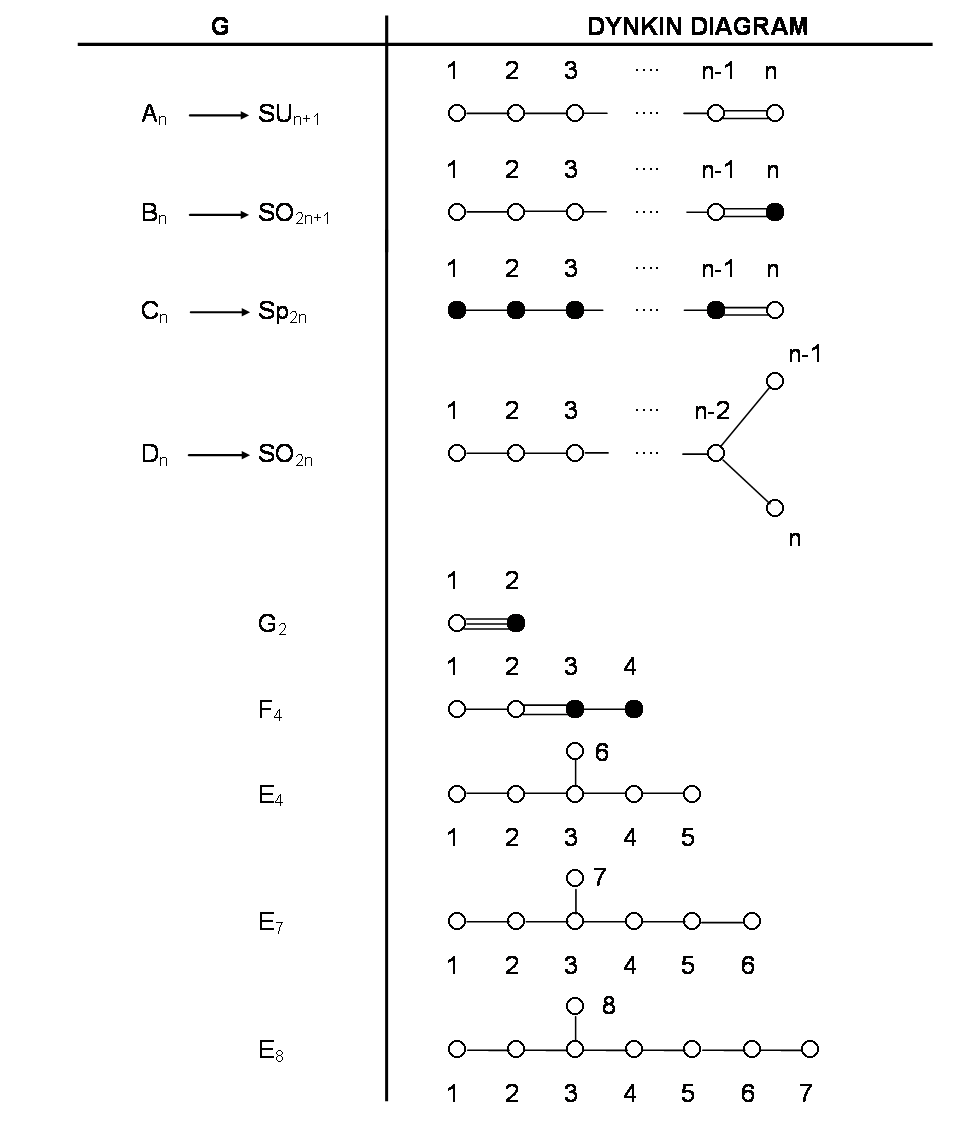 Suppose that G has N simple roots. There are
Suppose that G has N simple roots. There are= ½N(N-1) different pairs of root vectors (αi,α j) enclosing between them the angle θij. Therefore, the mutual orientation between the N root vectors in root space is specified completely by
angles. This number is the sum of the number of different pairs of orthogonal roots unjoined by a line in the Dynkin diagram of G and the number of pairs joined by one or more lines, which enclose any of the angles 120º, 135º or 150º. In the Dynkin diagram of every Lie algebra, there are no isolated roots: every simple root is joined to at least one other.
4
This means that there are=½(N-1) (N-2) right angles and
= (N-1) angles which are either 120º, 135º, 150º or mixtures thereof [N.B.
=
+
]. Tabulated below is the number of angles enclosed by all pairs of simple roots defining all possible Lie algebras:
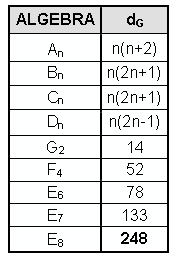
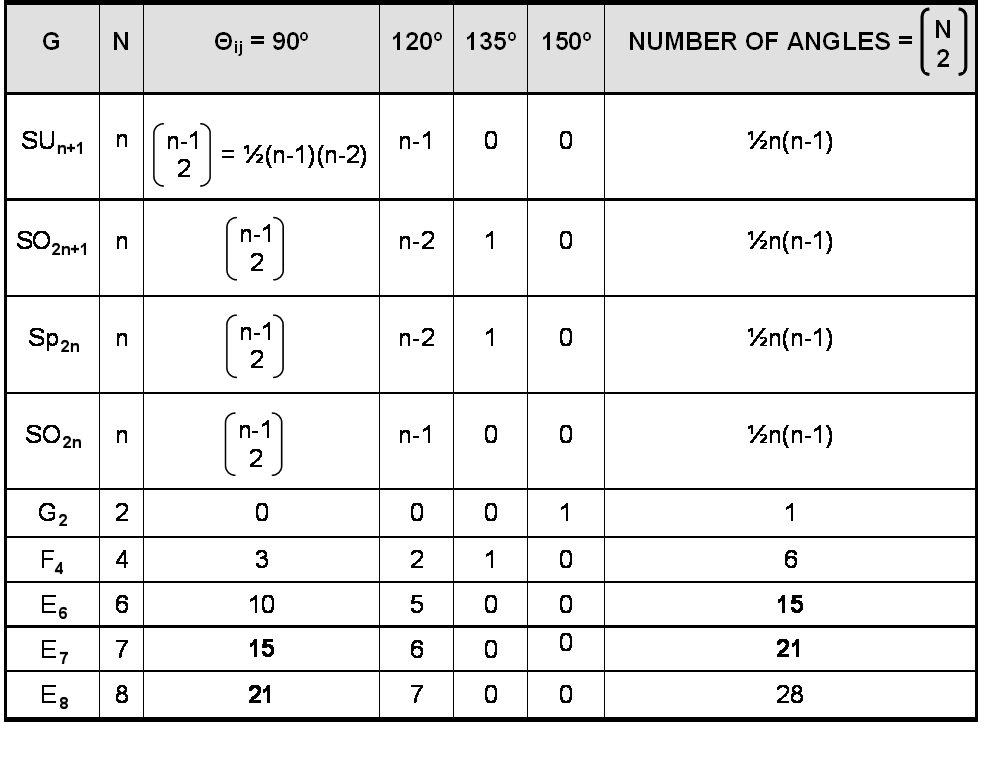 The Godname number 21 of Kether is the number of pairs of orthogonal roots of the superstring symmetry group E8 and the number of angles between the seven simple roots of E7. The Godname number 15 of Chokmah is the number of pairs of orthogonal roots of E7 and the number of angles between the six simple roots of E6, a subgroup of E8 favoured by many string theorists as the probable product of symmetry breaking of E8.
The Godname number 21 of Kether is the number of pairs of orthogonal roots of the superstring symmetry group E8 and the number of angles between the seven simple roots of E7. The Godname number 15 of Chokmah is the number of pairs of orthogonal roots of E7 and the number of angles between the six simple roots of E6, a subgroup of E8 favoured by many string theorists as the probable product of symmetry breaking of E8.
Turning to the non-exceptional groups:
1. for n = 6, number of angles between the simple roots of SU7, SO12, SO13 & Sp12 = 15;
2. for n = 7, number of right angles between the simple roots of SU8, SO15, SO14 & Sp14 = 15;
3. for n = 8, number of right angles between the simple roots of SU9, SO17, SO16 & Sp16 = 21.
Since the superstring symmetry group is E8, any other groups picked out by the Godnames of Kether or Chokmah must be subgroups of E8. These are: SU9, SO16 (n = 8), SU8 (n = 7) & SU7, SO13, SO12 (n = 6).
5
The dimension dG of G is the number of its generators. For what Lie algebra is dG = NGOD, where NGOD is a Godname number? The Lie algebras have the following dimensions:
None of the exceptional Lie algebras has a dimension that is a Godname number. Below are tabulated all values of n covering the range 15≤NGOD≤543, where 15 is the smallest and 543 is the largest Godname number: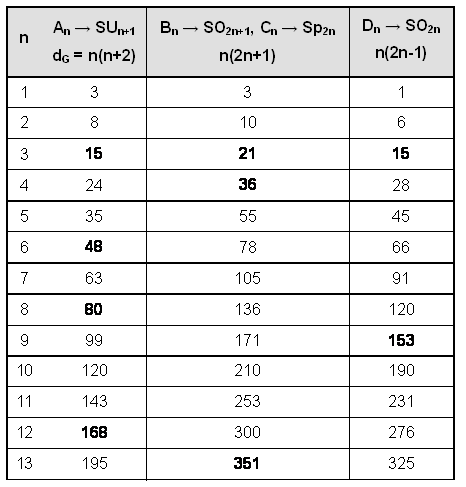
6
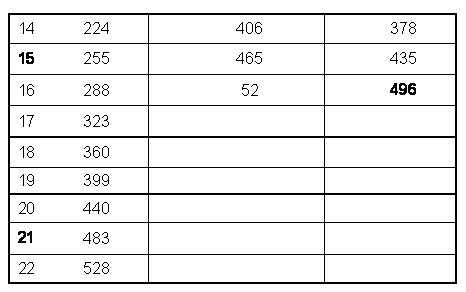 n = 16 determines the anomaly-free group SO32 with dimension 496. It is amusing that the dimension of SUn+1 exceeds the largest Godname number 543 for n>22, the number of Paths in the Tree of Life. B3, (SO7) and C3 (Sp6) have dimension 21, A3 (SU4) and D3 (SO6) have dimension 15, B4 (SO9) and C4 (Sp8) have dimension 36 and D9 (SO18) has dimension 153. Allowing the further kind of prescription:
n = 16 determines the anomaly-free group SO32 with dimension 496. It is amusing that the dimension of SUn+1 exceeds the largest Godname number 543 for n>22, the number of Paths in the Tree of Life. B3, (SO7) and C3 (Sp6) have dimension 21, A3 (SU4) and D3 (SO6) have dimension 15, B4 (SO9) and C4 (Sp8) have dimension 36 and D9 (SO18) has dimension 153. Allowing the further kind of prescription:
NGOD
NGOD NGODdG = NGOD NGOD NGODNGOD NGOD N GOD NGOD .i.e., 15 ≤dG≤ 5430, then B10 (SO21) and C10 (Sp20) have the dimension:2121 21dG = 21 21 21
21 21 21 21and SU19 has the dimension:3636 36dG = 36 36 3636 36 36 36(there are no other possibilities). The groups with rank less than or equal to the rank 8 of the superstring group E8 are SO7 and Sp6 (with dimension 21), SU4 and SO6 (with dimension 15), and SO9 and Sp8 (with dimension 36). SinceE8⊃SO16⊃SO9⊃SO7⊃SU4, E8⊃E6⊃Sp6⊃SU2×Sp6, and SU4≈SO6,
the Godname numbers 21, 15 and 36 define dimensions of subgroups of E8.
For what Lie algebras is the total number of angles between pairs of root vectors equal to NGOD, and what are their dimensions? Below are tabulated values of n determining NGOD and the corresponding dimension of the Lie algebra:7
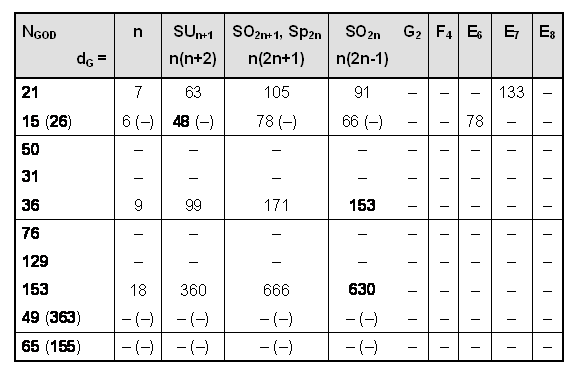 Godnames numbers of four Sephiroth each define four, non-exceptional Lie algebras:SO14 (91) SU8 (63)n = 7:
Godnames numbers of four Sephiroth each define four, non-exceptional Lie algebras:SO14 (91) SU8 (63)n = 7:= 21

Sp14 (105) SO 13 (78)SO12 (66) SU7 (48)n = 6:= 15
 Sp12 (78) SO 13 (78) (number in brackets is dimension of Lie algebra)SO18(153) SU10 (99)n = 9:
Sp12 (78) SO 13 (78) (number in brackets is dimension of Lie algebra)SO18(153) SU10 (99)n = 9:= 36
 Sp18 (171) SO19 (171)SO36 (630) SU19 (360)n = 18:
Sp18 (171) SO19 (171)SO36 (630) SU19 (360)n = 18:= 153

Sp36 (666) SO37 (666)21 also defines E7 and 15 defines E6. The Lie algebras corresponding to 153 have rank 18, which exceeds the rank 8 of E8 and the rank 16 of E8×E8 and SO32. They are therefore disallowed. The groups corresponding to 36 are also forbidden because they have rank 9. Only the Godname numbers 21 and 15 define groups of lesser rank than E8, all of which are its subgroups.
For what Lie algebras of rank N is the number of right angles between pairs of simple roots= NGOD, and what are their dimensions? Below are tabulated values of n
8
determining NGOD and the corresponding dimension dG of the Lie algebra: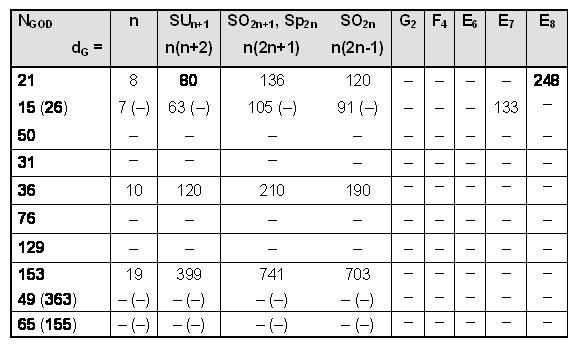 The Godname numbers of four Sephiroth (the same as above) define four non-exceptional Lie algebras:SO16(120) SU9( 80)n = 8:
The Godname numbers of four Sephiroth (the same as above) define four non-exceptional Lie algebras:SO16(120) SU9( 80)n = 8:= 21
 Sp16(136) SO17(136)SO14(91) SU8(63)n = 7:
Sp16(136) SO17(136)SO14(91) SU8(63)n = 7:= 15
 Sp14(105) SO15(105) (number in brackets is dimension of Lie algebra)SO20(190) SU11(120)n = 10:
Sp14(105) SO15(105) (number in brackets is dimension of Lie algebra)SO20(190) SU11(120)n = 10:= 36
 Sp20(210) SO21 (210)SO38(703) SU20(399)n = 19:
Sp20(210) SO21 (210)SO38(703) SU20(399)n = 19:= 153
 Sp38(741) SO39(741)Comments
Sp38(741) SO39(741)Comments
1. 21 also defines E8 and 15 defines E7, as found earlier. SO17 is excluded because SO16 is a maximal subgroup of E8. Since E8 contains the others as subgroups, the group selected by 21 with the largest dimension is E8.
2. 15 selects the rank-7 groups SU8, SO15, Sp14, SO14 and E7.
3. 36 selects only rank-10 groups, which are forbidden, having higher rank than E8.9
Similarly, the rank-19 groups selected by 153 are disallowed.
It is concluded that only 21 and 15 define groups of rank less than or equal to that of E8 whose numbers of orthogonal pairs of simple roots are equal to Godname numbers.
We shall now prove that the Godnames EHYEH and YAH have letter values that denote the numbers of right angles between sets of simple root vectors of E6, E7 and E8. Below are tabulated the Dynkin diagrams of these groups, their simple roots and the labelled simple roots that are perpendicular to them: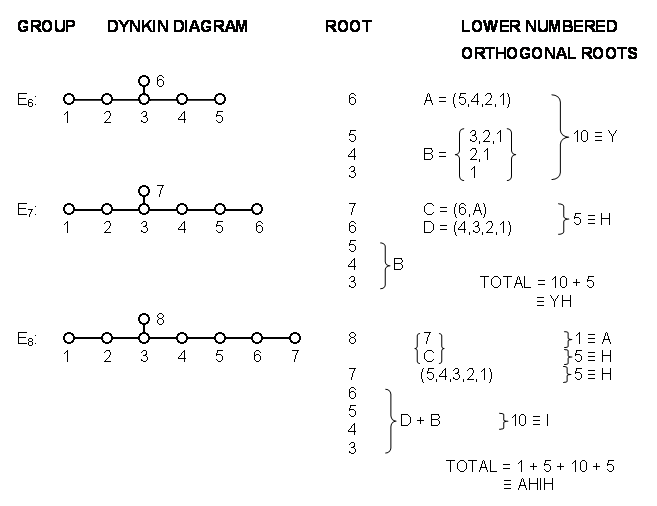 Notice that:
Notice that:
1. The number 15 of YAH (Hebrew: YH) is the number of right angles between the seven simple roots of E7. The value 10 of the letter Y is the number of right angles between the root vectors of E6 and the value 5 of letter H is the extra number of right angles between the simple root vectors of E7.
2. The number 21 of EHYEH (Hebrew: AHIH) is the number of right angles between the eight simple root vectors of E8. The value 1 of the letter A denotes the right angle between roots 8 & 7, the value 5 of the first letter H is the number of right angles between simple root 8 and simple roots 1, 2, 4, 5 & 6, and the value 5 of the second letter H is the number of right angles between simple root 7 and roots 1, 2, 3, 4 & 5. Comparing AHIH with YH and remembering that the Hebrew letters for I and Y are the same, we see that AHIH specifies the superstring symmetry group E8, YH specifies E7 and I (or Y) specifies E6.
According to the Dynkin diagram of E8, any simple root vector is orientated at an angle of 120º to one, two or three other simple root vectors. Compare the eight simple root10
vectors of E8 with one of the sets of eight generators of the (7+7) polygons enfolded in the Tree of Life: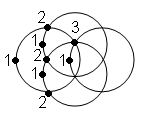 Each generator lies on one, two or three circles as the endpoint of a vertical or horizontal diameter. The simple root vector 3 is unique in being orientated at 120º to three other simple root vectors. Similarly, the generators located at Daath or Tiphareth in the Tree of Life are unique in being the points of intersection of three circles. The following correspondence emerges between the (7+1) simple root vectors of E8 and the seven Sephiroth + Daath of the Tree of Life:
Each generator lies on one, two or three circles as the endpoint of a vertical or horizontal diameter. The simple root vector 3 is unique in being orientated at 120º to three other simple root vectors. Similarly, the generators located at Daath or Tiphareth in the Tree of Life are unique in being the points of intersection of three circles. The following correspondence emerges between the (7+1) simple root vectors of E8 and the seven Sephiroth + Daath of the Tree of Life:
ROOT SEPHIRAH
8 → (Daath)
1 → Chesed
2 → Geburah
3 → Tiphareth
4 → Netzach
5 → Hod6 → Yesod
7 → Malkuth
Notice that the unique root vector 3 corresponds to Tiphareth, which uniquely occupies the centre of the Tree of Life both in a geometrical and in a metaphysical sense. This analogy between the generators of the polygons enfolded in the Tree of Life and the Dynkin diagram of the superstring group E8 should come as no surprise because, as we have already seen, the group mathematics of superstrings reflects the geometrical properties of the Divine Image, the cosmic paradigm of Creation.SUMMARY
Physicists use the mathematical language of group theory to describe the symmetries displayed by the four forces known to act between subatomic particles. Postulating that these symmetries exist at every point in space-time requires the existence of so-called 'gauge bosons.' These are quantum particles, the exchange of which between particles generates the force whose symmetry is described by the group in question. The number of gauge bosons associated with a gauge symmetry group describing a given kind of force is its dimension. Superstring theory predicts that the gauge symmetry group that accounts for all the forces (other than gravity) acting between superstrings must have a dimension of 496. The groups having this dimension are SO(32) and E8×E8, where E8 is the so-called 'exceptional group' with the largest dimension (248). A group is defined by its roots, the number of which is equal to its dimension. Each root can be expressed in terms of a set of so-called ‘simple roots,' which are depicted schematically by the Dynkin diagram of the group. The simple roots characterizing a group can be represented by finite straight lines that point in various directions in a mathematical space. The Dynkin diagram specifies both the lengths of these lines and the angles between them. Only four angles are possible: 90º, 120º, 135º & 150º. The number of right angles between the lines in this space representing the simple roots of E8 is 21, as11
is the total number of angles between the lines representing the simple roots of E7 (a group whose symmetries are part of the larger set of symmetries of E8). The number of right angles between the lines representing the simple roots of E7 is 15 , as is the total number of angles between the simple roots of E6 (a group that belongs to E8 as well). Hence, the Godname numbers of Kether (21) and Chokmah (15) prescribe the very gauge symmetry group (and two of its subgroups) that accounts for the unified force between superstrings.
2. YAH & YAHWEH prescribe 248 & 496
The dimension 248 of E8 and the dimension 496 of E8×E8 and SO(32) are determined in a purely arithmetic way by the two Godname numbers of Chokmah: YAH = 15 and YAHWEH = 26. It is instructive to analyse these arithmetic prescriptions in some detail because their existence is no fortuitous coincidence but, instead, arises from and reflects the beautiful, geometrical properties of the inner form of the Tree of Life.
The sum of the squares of the first 15 integers is
1240 = 12 + 22 + 32 + ... + 152.
This is a triangular array of integers 1–15. Therefore, 2480 (=2×1240) is the sum of a 16×16 square array of these integers shown in Figure 1 with a diagonal of zeros separating the two triangular arrays. It contains 256 (=44) integers comprising a diagonal row of 16 (=42) zeros and24
diagonal of zeros separating the two triangular arrays. It contains 256 (=44) integers comprising a diagonal row of 16 (=42) zeros and24
24 24
44 – 42 = 240 = 24 24 24 (24 = 1×2×3×4)
24 24 24 24non-zero integers 1, 2, 3... 15, where20 2 115 = 23 2 2
23 2 212
is the number of YAH. Remarkably, the square representation of the dimension of E8 also encodes as non-zero integers its number of non-zero roots. The Pythagorean Tetrad prescribes this arithmetic representation of the superstring parameter 248.
The identity:
4960 = 2×2480 = 4(12 + 22 + 32 + ... + 152).
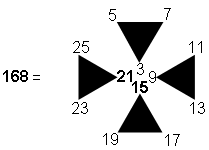
is represented in Figure 2 by a cross pattée array of integers 1, 2, 3... 15. The cross is made up of 480 integers, of which
integers form its boundary. Once again, the number 168 of the Mundane Chakra of
4960 =  Figure 2. Integers 1–15 in a cross pattée array sum to 4960.
Figure 2. Integers 1–15 in a cross pattée array sum to 4960.13
4960 =  Figure 3. Integers 1–15 in a St Andrews cross array sum to 4960.Malkuth appears in the context of the representation of the dimension of the superstring symmetry groups E8×E8 and SO(32) with dimension 496. This cross pattée representation of 4960 — the number of space-time components of the 496 gauge particles predicted by superstring theory — encodes the number 480 of non-zero roots of this group as the number of non-zero integers summing to 4960. Alternatively, a 31×31 square array of integers 1–15 in the form of a St. Andrews cross represents the number 4960 (Fig. 3). This demonstrates how the Godname EL with number value 31 prescribes the number of components of the gauge fields of superstrings.
Figure 3. Integers 1–15 in a St Andrews cross array sum to 4960.Malkuth appears in the context of the representation of the dimension of the superstring symmetry groups E8×E8 and SO(32) with dimension 496. This cross pattée representation of 4960 — the number of space-time components of the 496 gauge particles predicted by superstring theory — encodes the number 480 of non-zero roots of this group as the number of non-zero integers summing to 4960. Alternatively, a 31×31 square array of integers 1–15 in the form of a St. Andrews cross represents the number 4960 (Fig. 3). This demonstrates how the Godname EL with number value 31 prescribes the number of components of the gauge fields of superstrings.
The number of YAHWEH defines the dimension 248 of E8 in the following way: using the identity
6201 = 12 + 22 + 32 +… + 262,
then
24800 = 4×6200 = 4(22 + 32 +… + 262).
Figure 4 shows the cross pattée representation of this number. 1400 integers are present. The sum of the 296 integers forming the boundary of the cross is14
24800 =
 Figure 4. Integers 2–26 in a cross pattée array sum to 24800.
Figure 4. Integers 2–26 in a cross pattée array sum to 24800.15
331 331 331 331331 331 331 3315246 =
331 331 331 331
331 331 331 331,where 331 is the 67th prime number, 67 being the number value of Binah. Observe how, through this 4×4 square array representation, the Pythagorean Tetrad reveals that the number of Binah — the Sephirah embodying the most abstract archetypes of form — defines the shape of an archetypal pattern of numbers whose sum characterizes the physics of superstrings! Since 24800 is the sum of 1400 integers, 49600 is the sum of 2800 integers, where
280
280 280
2800 = 280 280 280
280 280 280 280 ,
thus relating the second perfect number 28 to the third perfect number 496 as well as the number 496 of Malkuth to the number value 280 of Sandalphon, its Archangel. All these representations of 248 and 496 in terms of the two Godname numbers of Chokmah have a four-fold, rotational symmetry: their appearance is unaltered by a rotation of 90º. They illustrate the fundamental importance of the Pythagorean Tetrad in expressing parameters of the Tree of Life.
3. Godnames of Hod & Netzach prescribe 248 & 496
It should not be supposed that only two of the ten Godname numbers prescribe the dimensions of the superstring gauge symmetry groups E8, SO(32) and E8×E8. The Godnames of all the Sephiroth participate in this prescription, their specificity increasing, the lower the position of the Sephirah in the Tree of Life. As an example, we shall now consider how the numbers of the Godnames YAHWEH SABAOTH of Netzach and ELOHIM SABAOTH of Hod conspire to determine the numbers 248 and 496.
The identity26
24800 = Σ (2n) 2 = 42 + 62 + 82 + ... + 522.
n=2can be written as follows in terms of the odd integers composing each square number in this summation:
4 2 = 1 + 3 + 5 + 7.
6 2 = 1 + 3 + 5 + 7 + 9 + 11.
8 2 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 .
●
●
52 2 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 +...+ 101 + 103 .
Adding,24800 = 25(1+3+5+7) + 24(9+11) + 23(13+15) + ... + 1(101+103).
The number 24800 is the sum of a stack of 26 pairs of odd integers, the base of which comprises 25 ‘1's and the apex of which is the number 103. Figure 5 shows two similar16
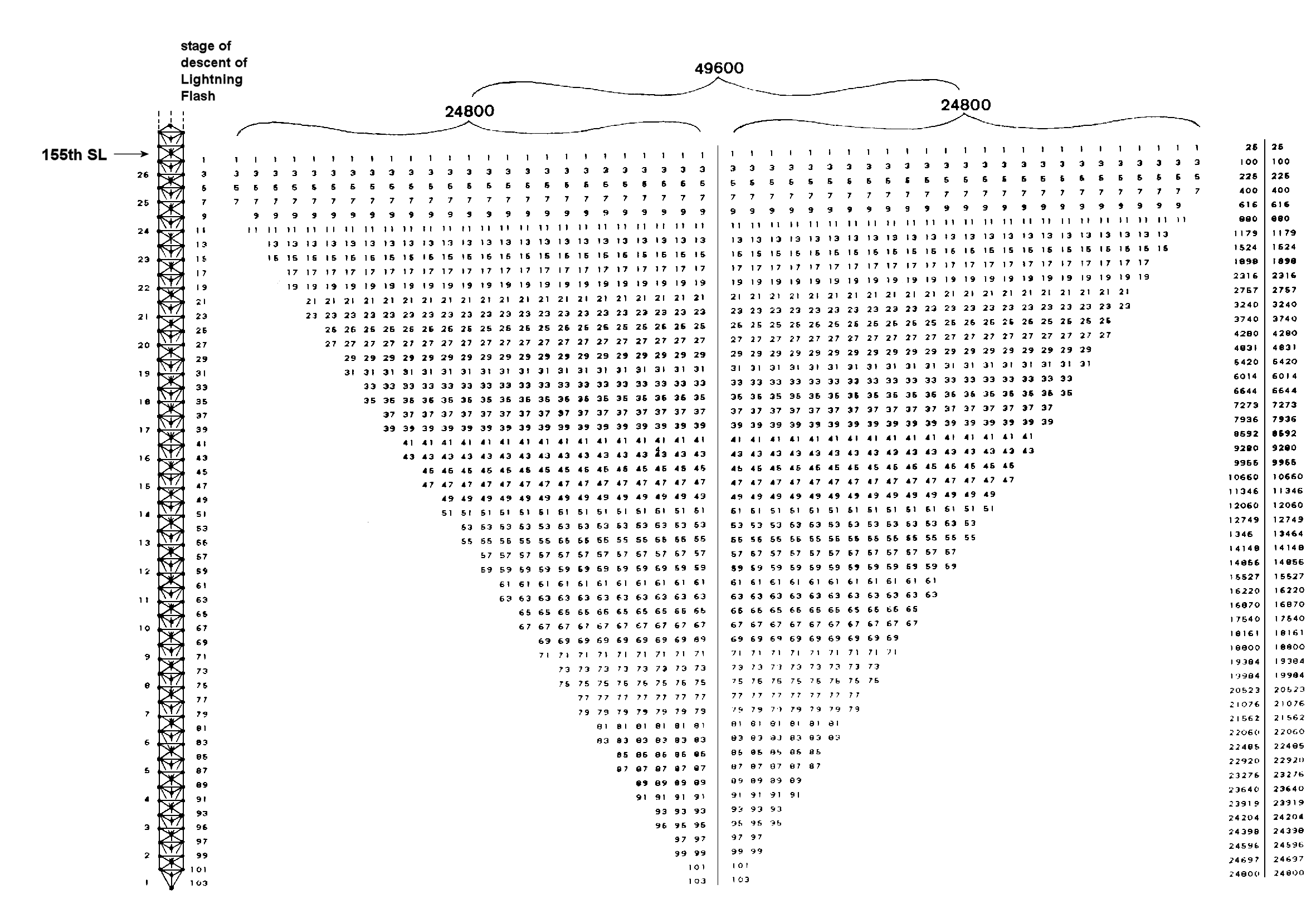 Figure 5
Figure 517
stacks placed side by side to represent the number 49600. The reason why they are depicted as inverted will be given shortly. The base of the pair of stacks consists of 50 ‘1's. The height and width of the pair of stacks is prescribed by the numbers of, respectively, YAHWEH and ELOHIM. The range of integers is specified by the number 103, which is the number of SABAOTH ("Hosts"). Each stack is prescribed by YAHWEH SABAOTH, whilst both stacks are prescribed by ELOHIM SABAOTH. This is how these two Godnames define patterns of integers adding up to 24800 and 49600. Ignoring the factor of 100, which merely reflects the 10‑dimensional nature of superstring space-time, we see that the number 496 naturally splits up into two 248s, reproducing what mathematicians call the "direct product" of two similar E8 groups with dimension 248. These Godnames prescribe in an arithmetic way the E8×E8 heterotic superstring.
The number of yods in the n-tree (the lowest n Trees of Life) with all their triangles turned into tetractyses is given by
Y(n) = 50n + 30.The 49-tree represents what Theosophists call the "cosmic physical plane," each Tree mapping one of its 49 subplanes. It has Y(49) = 2480 yods. This is the number of space-time components of the 248 10-dimensional gauge fields of E8. It can be pressed as the sum
4 4
2480 = Σ t n + Σ T n ,
n=0 n=1where
4 n 1 n
3 n 3 n 2 n 2 n
t n = 2 n 2 n 2 n and T n = 3 n 3 n 3 n
1n 1 n 1 n 1 n 4 n 4 n 4 n 4 n.
It is remarkable that the number of integers in each stack summing to 24800 is
3
700 = Σ (t n + Tn) ,
n=1which is the number of yods in ten separate Trees of Life whose triangles are tetractyses. As well as illustrating the basic designing role of the Pythagorean Decad, this shows how yods can denote things such as numbers when they collectively define a Tree of Life parameter like the number 248.
The column of numbers on the right-hand side of Figure 5 is the running total of the integers in successive rows of either stack, addition commencing from the top row. Three partial sums are multiples of 100. The first two rows sum to 100, the first four rows sum to 400 and the first 36 rows add up to18800, after which a further 72 integers in 16 rows sum to 6000, making a total of 24800. The Godname number 36 of Geburah specifies a point in the summation of rows of integers yielding a partial sum that is a multiple of 100. Being specified by the number of a Godname, this stage has significance vis-à-vis the Tree of Life, as we now explain. There are 103 stages of descent of the Lightning Flash from Kether of the 25th Tree, which, as the 155th SL, prescribed by the Godname ADONAI MELEKH of Malkuth. The first stage of descent reaches Hod of the 26th Tree, the 153rd SL specified by ELOHIM SABAOTH with number value 153. By comparing stages of descent of the Lightning Flash in the 26-tree
18
shown on the left in Figure 5 with the integers 1, 3, 5 ... 103, it will be seen that, for example, the 9th and 11th stages of descent occur at the Lower Face of the 24th Tree, the 13th and 15th stages occur at the Lower Face of the 23rd Tree, etc. In other words, the integers in the paired rows of the stacks are, simply, the numbers of stages of descent of the Lightning Flash in successive Trees. The 71st stage of descent, at which the running sum of the first 36 rows of integers is 18800, reaches Chesed of the eighth tree, which is the 49th SL in the Cosmic Tree of Life. The Godname number of Yesod specifies the row where the partial sum is a multiple of 100 and therefore of possible physical significance. This is why we have considered an inverted stack of integers.
The summation of odd integers given above leading to the number 24800 has a simple interpretation vis-à-vis the 26-tree that is the counterpart of 26-dimensional space-time. Noting that: 1 + 3 = 2×2, 5 + 7 = 2×6, 9 + 11 = 2×10, etc., 24800 can be written:24800 = 50×2 + 50×6 + 48×10 + 46×14 +... + 4×98 + 2×102
25
= 50×2 + Σ 2n(106 – 4n).
n=1
This is the sum of the numbers of SLs on the central pillar up to Yesod of each successive Tree, each number being weighted with the number of stages of descent of the Lightning Flash from the 155th SL specified by ADONAI MELEKH to that Yesod. The additional term 50×2 is t he product of the number (50) of SLs on the central pillar up to Yesod of the 25th Tree and the number (2) of stages of descent of the Lightning Flash from the 155th SL to Yesod of the 26th (not the 25th) Tree. Its difference from the other terms correlates with the fact that the 26th Tree is the counterpart of the dimension of time, whereas lower Trees correspond to dimensions of space.
Yesod of the nth tree is the 2nth SL on the central pillar. The Lightning Flash descends in (4n–3) stages from this SL. So the number of stages of descent from Kether of the 25th Tree to this SL = 103 – (4n–3) = 106 – 4n. The sum:
25
24700 = Σ 2n(106 – 4n)
n=1
The sum of the (700+700) integers in the two stacks is49600 =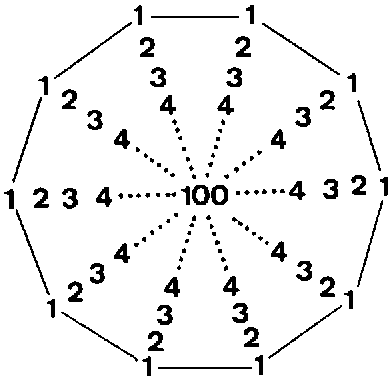 10 = 1 + 2 + 3 + 4
10 = 1 + 2 + 3 + 4
100 = 13 + 23 + 33 + 43This 10-fold array of integers 1–100 is a beautiful illustration of how the Pythagorean Decad and integers 1, 2, 3 & 4 define this superstring number. The sum of the rows of the twenty-five ‘1's and twenty-five ‘3's = 100 = 13 + 23 + 33 + 43. The number of integers 5–103 in the 50 remaining rows of a stack is6565 65 t 2 T2 543 26
650 = 65 65 65 ==

65 65 65 65 t3 T3 31 5019
where 65 is the number value of ADONAI, the Godname of Malkuth, and 543, 26, 50 & 31 are the number values of the Godnames of the first four Sephiroth, illustrating once more the defining role of the Tetrad. Their sum is
2470
2470 2470
24700 = 2470 2470 2470
2470 2 470 2470 2470,
where
4
2470 = Σ (t n + Tn) = 12 + 22 + 32 + ... + 192.
n=1
The number of integers 5–103 in the remaining (50+50) rows of both stacks = 1300 = 26×50 = 15 + 25 + 35 + 45
14
24 24
= 34 34 34
44 4 4 4 4 44 .
This illustrates the Tetrad Principle, through which archetypal patterns of numbers such as that in Figure 5 are prescribed by the number 4. Their sum is
4
49400 = (13 + 23 + 33 + 43) Σ (1n + 2n + 3n + 4n ) .
n=1
The number of integers on the edge of each stack is 76, demonstrating how the Godname number of Tiphareth also defines the number 24800. It is remarkable that the sum of the 152 integers on the boundary of both stacks is 5456 because this is the sum of the first 31 triangular numbers. This shows how the Godname EL of Chesed with number value 31 prescribes the pattern of integers generating the number 24800.
Another way of seeing how ELOHIM, the Godname of Binah, prescribes the number 24800 and thus the dimension 248 of the superstring symmetry group E8 is as follows: any square number n2 is the sum of the (n–1)th and (n+1)th triangular numbers because
n2 = ½(n–1)n + n(n+1).
Applying this property to the squares of the 25 integers 4, 6, 8... 52:
42 = 6 + 10.
62 = 15 + 21.
82 = 28 + 36.
●
●
●
522 = 1326 + 1378.
The sum:
24800 = 42 + 62 + 82 + ... + 522
20
is the sum of the first 50 triangular numbers after 3. Therefore, the number of ELOHIM prescribes the number 248 as the ‘kernel’ of 24800. Since 24800 = 496×50, the crucial dimension 496 of any gauge symmetry group that is free of quantum anomalies is the arithmetic mean of the first 50 triangular numbers after 3. This is the remarkable way in which ELOHIM prescribes the number of gauge fields that mediate the unified superstring interaction.
Finally, the number 155 of ADONAI MELEKH, the Godname of Malkuth, is related by the Pythagorean Tetrad to the number 248 by
155 = 1+2+3+4 × 248.42In other words, a 4×4 square array of the number value of ADONAI MELEKH generates the 2480 space-time components of the 10-dimensional fields of the 248 gauge bosons of E8. This fact demonstrates the profound Pythagorean principle whereby the Tetrad and its geometrical symbol — the square — express the basic, physical properties of nature.
21