ARTICLE 13
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
Not only are there seven notes of the Pythagorean musical scale but also seven types of 36 groups of notes can be played using a tetractys array of ten notes. These groups constitute a Tree of Life pattern because they correspond to the 36 corners of the seven enfolded polygons in each half of the inner form of the Tree of Life. The same is true for the 524 ways in which the ten notes can be played to create 5–10 sounds, for they correspond to the 524 yods of the whole inner Tree of Life. These sequences include 240 sequences of 10 notes and 240 sequences of eight, nine and 10 sounds. Tetractys arrays of the ten octaves of each note of the Pythagorean scale generate 1680 sequences of ten notes, that is, 16,800 notes. This musical pattern is similar to the 16800 spirillae in the ten whorls of the heterotic superstring described over a century ago by Annie Besant and C.W. Leadbeater. It suggests that the heterotic superstring of ordinary matter is like a ten-stringed harp whose 240 musical sequences (actually ten sets of 24) correspond to 240 gauge charges of the superstring symmetry group E8 spread out over its length, each set of 24 sequences being analogous to the 24 charges carried by each of the 10 whorls of the superstring. The analogy predicts that the heterotic superstring of shadow matter consists of five whorls with 12600 spirillae. The E8×E8 heterotic superstring is like a self-playing, musical instrument whose states are its score and whose unified force described by E8 is the music that it makes. |
1
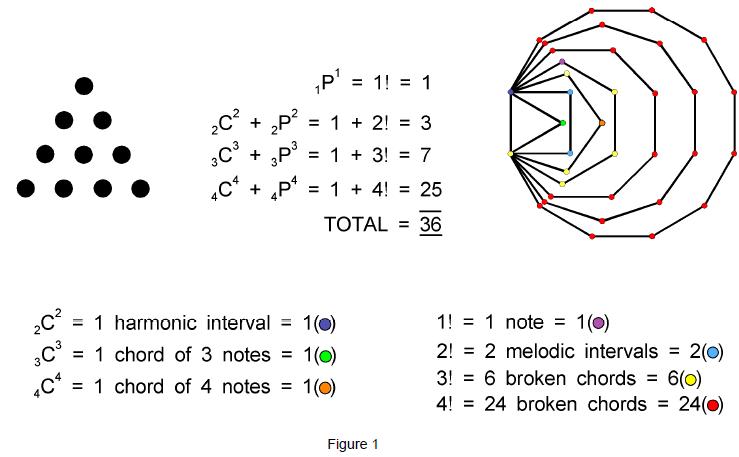
THE 36 CORNERS OF THE 7 ENFOLDED POLYGONS DENOTE THE 36
MUSICAL ELEMENTS THAT A TETRACTYS OF 10 NOTES CAN PLAY2
1. Musical potential of tetractys of notes
Consider a tetractys array of 10 notes of the Pythagorean scale labelled by letters of the alphabet:
1
2
3
4A
B C
D E F
G H I JWhat these notes are need not be known at this point; they will be specified later. A combination of notes played together defines a harmonic interval or a chord and their various permutations played in succession define melodic intervals and broken chords. The rule for playing a tetractys of notes is: starting with note A, the 10 notes are played in four stages, each one using all the notes in a row and not notes in other rows. There are seven types of basic musical elements, or ‘sounds’: the starting note A (written ‘1’), a harmonic interval formed from B & C (written ‘2’), a melodic interval formed from notes B & C (written ‘2’), a chord (written ‘3’) and a broken chord (3) formed from D, E & F and a chord (4) and broken chord (4) formed from G, H, I & J. The numbers of sounds playable at each stage are listed below:
1 1C1 =
(1)
2 (2 & 2×2) 3 (3 & 6×3) 4 (4 & 24×4) ELOHA, the Godname of Geburah with number value 36 (1) prescribes how many basic harmonies and melodies can be played by using the notes in each row of the tetractys. 36 is also the number of corners in the seven enfolded polygons forming each half of the inner form of the Tree of Life. Figure 1 shows how the numbers of the seven types of sounds correspond to the corners of these polygons. The number of ways (‘musical sequences’) the 10 notes can be played = 1×3×7×25 = 525. Of these, the musical sequence 1.2.3.4 consists of four sounds, the least number of sounds that the tetractys can play. The 524 musical sequences comprising 5-10 sounds are listed below:
Musical sequence
Number of sounds
Number of musical sequences
Number of sounds
1. 1.2.3.4
3
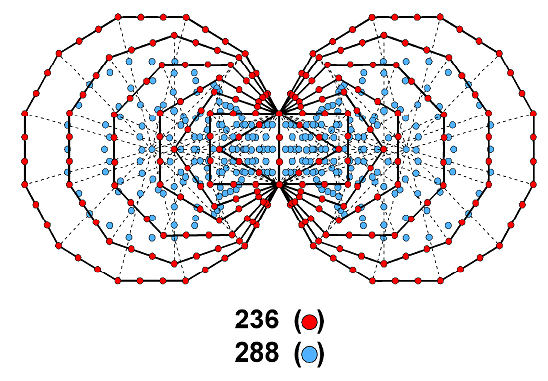
Figure 2. The (7+7) enfolded polygons have 236 yods on their boundaries and 288 yods inside them.
4
2.
3.
1.2.3.4
1.2.3.4
1 + 1 + 3 + 4 = 9
1 +2 + 1 + 4 = 8
1×1×3!×4! = 144
1×2!×1×4! = 48
44×9 = 1296
48×8 = 384
SUBTOTAL = 480
SUBTOTAL = 4560
4.
5.6.
7.
1.2.3.4
1.2.3.4
1.2.3.4
1.2.3.4
1 + 1 + 1 + 4 = 7
1 + 2 + 3 + 1 = 7
1 + 1 + 3 + 1 = 6
1 + 2 + 1 + 1 = 5
1×1×1×4! = 24
1×2!×3!×1 = 12
1×1×3!×1 = 6
1 ×2!×1×1 = 2
24×7 = 168
12×7 = 84
6×6 = 36
2×5 = 10
SUBTOTAL = 44
SUBTOTAL = 298
TOTAL = 524
TOTAL = 4858
As in the case of the sounds playable with a tetractys, the 524 musical sequences are of seven types. (24+12=36) sequences of two types contain the same number (7) of sounds and (524–36=488) sequences of five types contain different numbers of sounds. The latter comprise two sequences (1. 2.3.4 ) of five sounds, six sequences (1.2.3.4) of six sounds and 480 sequences of eight, nine & 10 sounds that terminate in broken chords of four notes. Of the latter,
288 (=1!×2!×3!×4!) are sequences of 10 successive notes (note, melodic interval & two broken chords). The division:
524 = 288 + 236
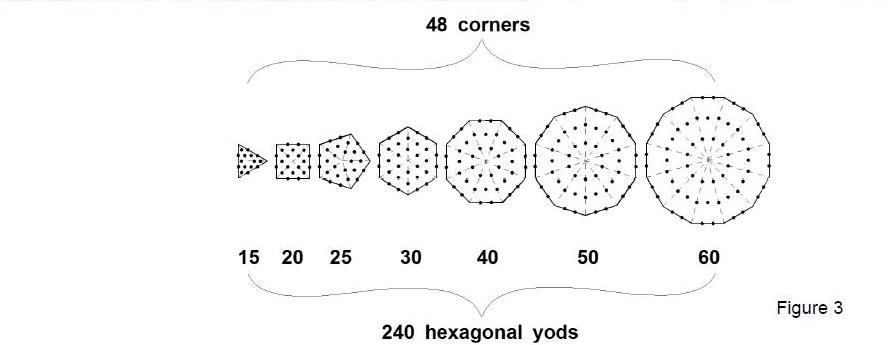
between the number of sequences of 10 notes and the number of sequences of 5-9 sounds has its counterpart in the (7+7) enfolded polygons, which have 236 yods on their boundaries and 288 yods inside them (Fig. 2). Furthermore, 288 yods surround the centres of the seven separate polygons, of which 48 are corners and 240
5
6
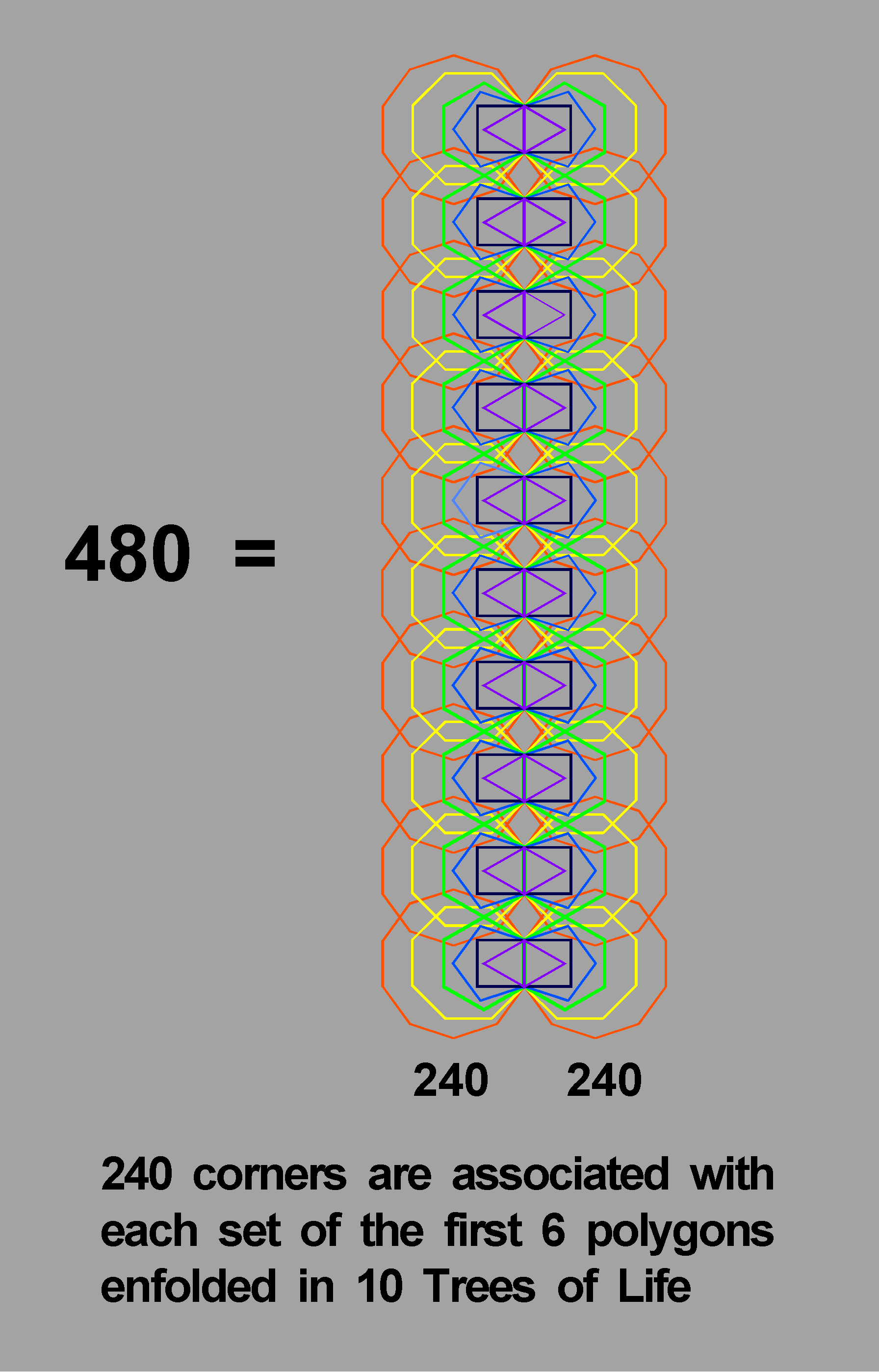
Figure 5. 480 corners are intrinsic to the first (6+6) polygons enfolded in 10 Trees of Life.
7
8
are hexagonal yods (Fig. 3). This division:
288 = 48 + 240
= 2×4! + 10×4! = 12×4!
characterises a Tree of Life pattern whose counterpart for the tetractys of notes are the 12×4! sequences (1.2.3.4) of 10 notes, two of which contain five notes in the rows of two and three played in either ascending or descending pitch and 10 of which contain such notes with both ascending and descending pitch. This means that the 480 sequences split into 10 sets of 24 sequences of 10 notes, totalling 2400 notes, and 48, 144 and 48 sequences of, respectively, eight, nine and 10 sounds, making a total of 2160 sounds in 240 more sequences. (2400+2160=4560) sounds are played in the 480 sequences.
The number of yods in n overlapping Trees of Life is:
Ỹ(n) = 50n + 20.
The 91 trees of CTOL have Ỹ(91) = (50×91 + 20 = 4570) yods. There are 10 yods in CTOL arranged in a tetractys down to the path connecting Chokmah and Binah of the 91st tree. Below the highest Binah in CTOL are therefore 4560 yods, that is, the number of yods in 456 tetractyses. Supposing that these 10 highest yods in CTOL symbolised 10 notes of the Pythagorean scale, then each yod below the Supernal Triad of the highest tree would symbolise a sound made during the playing of the 480 sequences! This amazing property is indicative of the archetypal character of these sequences, which are the counterpart of the (240+240=480) hexagonal yods of the (7+7) separate polygons (Fig. 3).
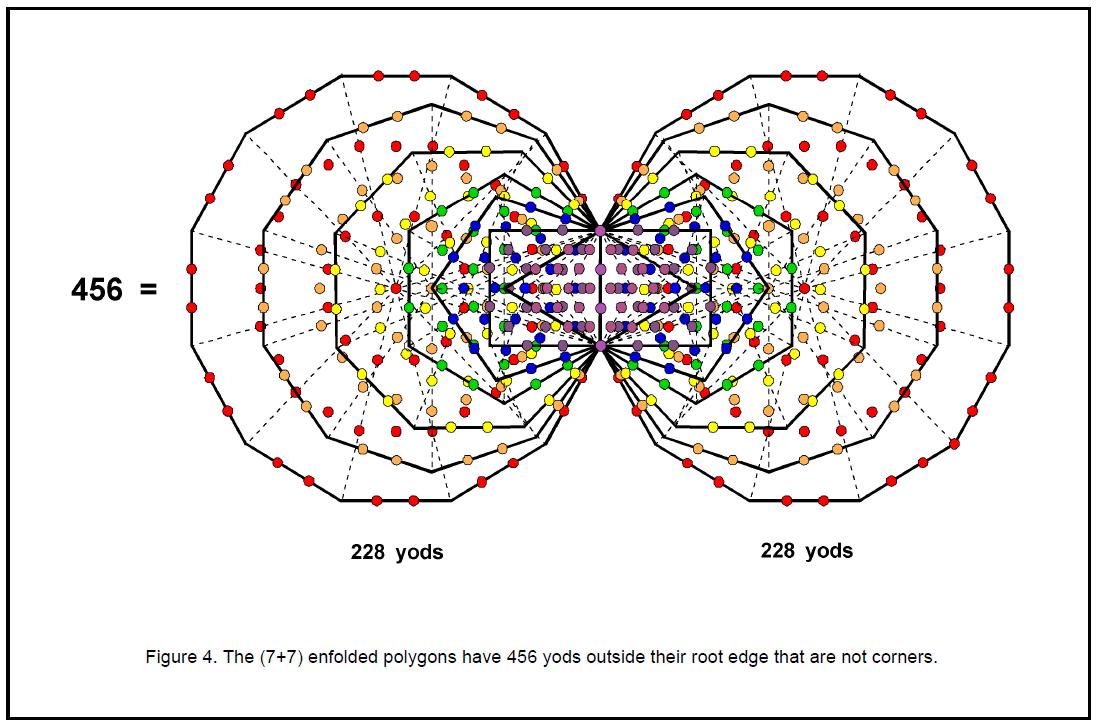
Further evidence of these 480 sequences constituting a Tree of Life pattern is as follows: the (7+7) enfolded polygons have 70 corners, that is, 68 corners outside their root edge. The number of yods that are not external corners = 524 – 68 = 456 (Fig. 4). The (70+70) polygons enfolded in 10 overlapping Trees of Life therefore have 4560 such yods. Each set of 70 polygons has 351 corners. 351 is the number value of Ashim, the Order of Angels assigned to Malkuth. This, as well as other Godnames, Archangelic names, etc, characterise the inner form of 10
9
overlapping Trees of Life that contain 4560 yods other than corners outside their shared edges. The division
480 = 240 + 240
is present in the inner form of 10 overlapping Trees of Life as the (240+240) corners of the first (6+6) polygons enfolded in them (Fig. 5).
We have seen that playing a tetractys of 10 notes to create 8, 9 and 10 sounds generates 480 musical sequences with 4560 sounds. Suppose now that the same 10 notes are played in a similar way in the three possible orientations of the tetractys. This generates (3×480=1440) sequences of 8, 9 &
10
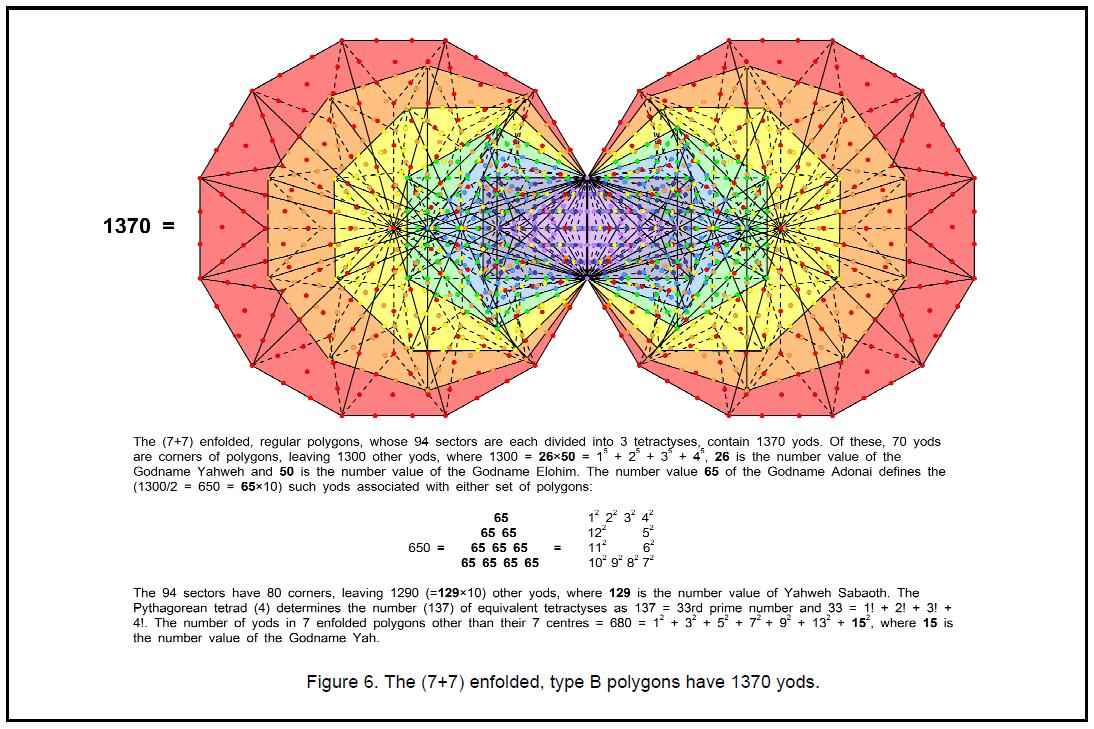
10 sounds with (3×4560=13680) sounds. The (7+7) enfolded, type B polygons have 1370 yods (Fig. 6), two of which are the topmost corners of the two hexagons shared with the lowest corners of the hexagons enfolded in the next higher tree. The number of yods in all the polygons enfolded in the n-tree = 1368n +2. There are therefore 13680 yods intrinsic to the polygons enfolded in the 10-tree, that is, yods unshared with polygons enfolded in the 11th tree. This shows
that the full musical potential of a tetractys of 10 notes is encoded in the inner form of 10 Trees of Life representing the 10 Sephiroth of a single tree. Because the tetractys and
Table 1. Table of tone ratios
| C | D | E | F | G | A | B | |
| 1 | 1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 |
| 2 | 2 | 9/4 | 81/31 | 8/3 | 3 | 27/8 | 243/64 |
| 3 | 4 | 9/2 | 81/16 | 16/3 | 6 | 27/4 | 243/32 |
| 4 | 8 | 9 | 81/8 | 32/3 | 12 | 27/2 | 243/16 |
| 5 | 16 | 18 | 81/4 | 64/3 | 24 | 27 | 243/8 |
| 6 | 32 | 36 | 81/2 | 128/3 | 48 | 54 | 243/4 |
| 7 | 64 | 72 | 81 | 256/3 | 96 | 108 | 243/2 |
| 8 | 128 | 144 | 162 | 512/3 | 192 | 216 | 243 |
| 9 | 256 | 288 | 324 | 1024/3 | 384 | 432 | 486 |
| 10 | 512 | 576 | 648 | 2048/3 | 768 | 864 | 972 |
11
the Tree of Life are equivalent symbols of the 10-fold nature of Divine Unity, what is numerically embodied in the former has to be identical to what is geometrically represented in the inner form of the latter.
2. Comparison with the heterotic E8×E8' superstring
Table 1 shows the 70 notes of 10 successive octaves of the Pythagorean scale. They constitute a Tree of Life pattern because, when converted into tetractyses, the 16 triangles making up a Tree of Life contain 70 yods (Fig. 7). The division of the 70 notes into the 35 notes of the first five octaves and the 35 notes of the next five octaves corresponds in the Tree of Life to the distribution of 35 yods making up its trunk* (shown in Fig. 7 as (
) yods) and 35 (
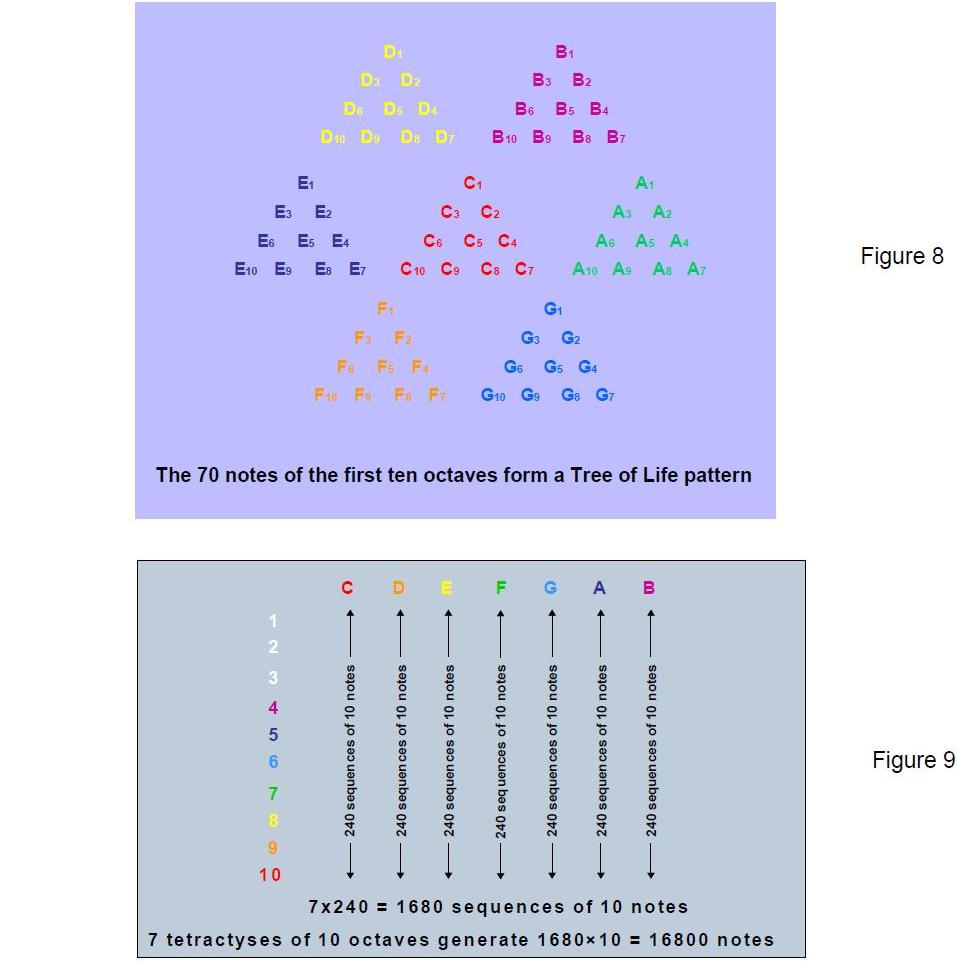
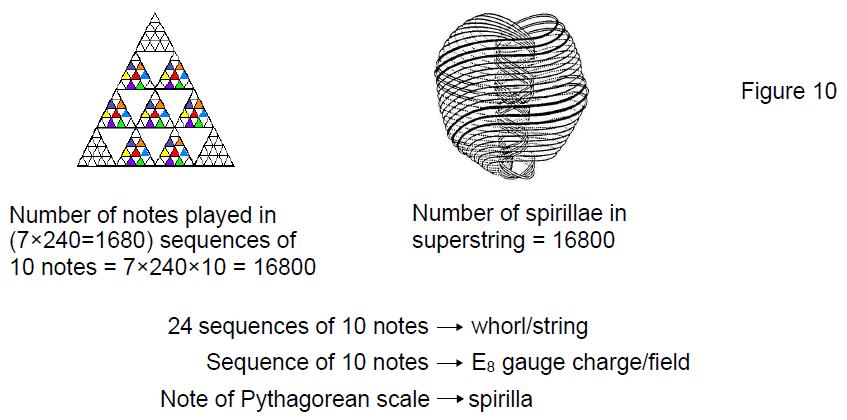
) yods outside it. Playing these notes arranged in seven tetractys arrays of the 10 octaves of each note of the Pythagorean scale (Fig. 8) generates (7×240=1680) musical sequences of 10 notes, making 16800 notes.
Compare this result with the fact that the UPA superstring described over 100 years ago by Annie Besant and C.W. Leadbeater consists of 10 whorls, each with 1680 spirillae, totalling 16800 spirillae. A whorl is analogous to an octave, spirillae in different whorls corresponding to different octaves of the same note. Each note of the Pythagorean scale has 240 sequences of its 10 octaves (Fig. 9), the counterpart of which are sets of 240 spirillae in each whorl, repeated seven times. The 240 musical sequences for each note of the Pythagorean scale consist of 10 sets of 24 sequences of 10 notes. The 1680 sequences for all seven notes therefore comprise 10 sets of (7×24=168) sequences of 10 notes, that is 10 sets of 1680 notes (Fig. 10). The 1680 circularly polarised oscillations in each of the 10 string components of the superstring of ordinary matter have as their musical counterpart these 168 cycles. Fittingly, 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, signifying the physical manifestation of the Tree of Life.
The superstring counterpart of the 480 musical sequences of 8, 9 & 10 sounds is the 480 gauge charges of the gauge symmetry group E8×E8' for the heterotic superstring corresponding to its 480 non-zero roots. The 240 musical sequences 1.2.3.4 of 10 sounds match the 240 gauge charges corresponding to the 240 non-zero roots of the
* The trunk of the Tree of Life is the geometrical sequence of point (Kether), line (Binah–Chokmah path), triangle (Chesed, Geburah & Tiphareth at its corners) and tetrahedron (Netzach, Hod, Yesod & Malkuth at its corners).
12
gauge symmetry group E8 for superstrings of ordinary matter. The 240 sequences:
|
1.2.3.4 |
48 sequences of 10 sounds |
correspond to the 240 gauge charges associated with the 240 non-zero roots of the gauge symmetry group E8' for heterotic superstrings of shadow matter. 2160 sounds are created by the 240 ways of playing a tetractys of 10 notes to generate eight, nine & 10 sounds. 216 is not only the 55th note, where 55 is the 10th triangular number, but also the 26th whole tone ratio (2), showing how the Godname YAHWEH with number value 26 prescribes this number in the context of shadow superstrings. 216 is the number of Geburah, whose Godname number (36) is the number of different musical elements playable with a tetractys of 10 notes. (7×2160=15120) sounds are made by the 1680 ways of playing tetractys arrays of 10 successive octaves of the seven notes of the Pythagorean scale. As each spirilla of the superstring of ordinary matter corresponds to a note in the 1680 sequences of 10 sounds. This suggests that the
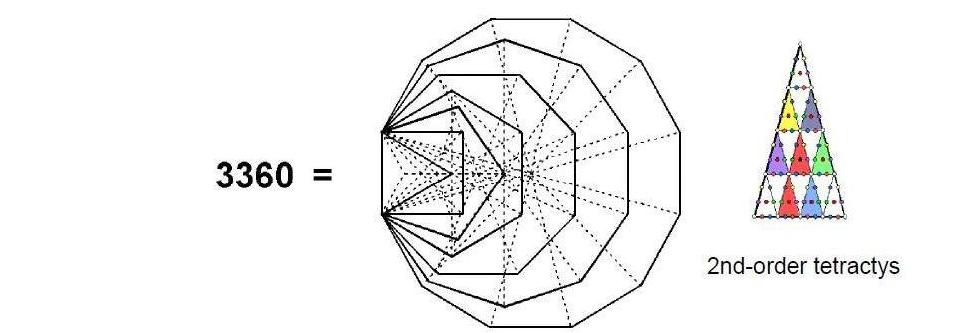
Figure 11 The number of spirillae in one of the whorls of the shadow superstring is encoded in the Tree of Life blueprint as the yod population of the seven enfolded polygons with 2nd-order tetractyses as their sectors.
shadow superstring is made up of 15120 spirillae instead of 16800 spirillae. As 15120 = 70×216, this number is generated by assigning the number value 216 of Geburah to each of the 70 yods making up the Tree of Life. Unlike ordinary superstrings, however, where the sounds played in each sequence are the notes of the 10 octaves, this number is, in the case of shadow superstrings, not the same for the different types of sequences. This
13
means that the sounds cannot correspond evenly to their whorls for each of the 1680 sequences. There are (7×48=336) sequences of 10 sounds, 336 sequences of eight sounds and (7×144=1008=3×336) sequences of nine sounds. Supposing that 336 sequences correspond to a whorl, then the shadow superstring consists of five whorls instead of 10 whorls, one comprising (10×336=3360) spirillae, one consisting of (8×336=2688) spirillae and three consisting of (9×1008=9072) spirillae, that is, 3024 in each one. 3360 is the number of spirillae on average in each of the five revolutions of the UPA superstring. It is encoded in the inner form of the Tree of Life as the number of yods in the seven enfolded polygons when their 47 sectors are turned into 2nd-order tetractyses (Fig. 11). The 1680 sequences of eight, nine & 10 sounds produce a total of 15120 sounds corresponding to which are the 15120 spirillae of the shadow
superstring, whilst the 1680 sequences of 10 notes produce 16800 notes, corresponding to which are the 16800 spirillae of the ordinary superstring. The analogy between the musical potential of the tetractys and the oscillatory nature of the heterotic superstring of ordinary matter enables one to predict the form of the heterotic superstring of shadow matter.
The conclusion that shadow superstrings have five whorls agrees with the prediction made in Article 2 that they consist of five string-like components.
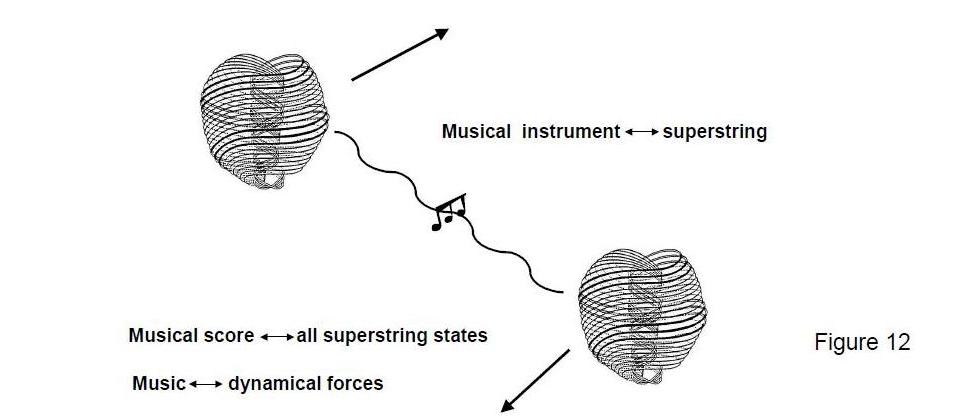
The picture that emerges from this comparison of the heterotic superstring described by Besant and Leadbeater with the musical potential of a tetractys of notes drawn from 10 octaves of the Pythagorean scale is that superstrings are a kind of musical instrument — like a harp with 10 strings which, when plucked according to the rules given earlier,
14
create all possible harmonic and melodic forms composed of up to four notes of the Pythagorean scale. The oscillations corresponding to them determine both superstring structure and dynamics. Superstrings are the musical instrument and their forces are like the sound vibrations that the latter emit (Fig. 12). The incessant interaction between superstrings, mediated by the exchange of the E8 gauge particles, is an unheard symphony of ‘sound’ transmitted between these instruments. The photons of light emitted and absorbed by the electrons inside atoms would be the most common sound of this symphony, for these quanta of the electromagnetic field are but one of the gauge fields of the superstring gauge symmetry group E8. Each whorl would represent 24 sequences of a tetractys of 10 octaves of each note of the Pythagorean scale. Those forces of nature expressed by the 240 gauge fields associated with the non-zero roots of E8 have their 240 gauge charge sources in the whorls/string components of the E8×E8 heterotic superstring, these charges being spread out over the strings as the counterparts of the 240 musical sequences that can be played with a tetractys of 10 octaves of each note of the Pythagorean scale. It is as if the basic forces acting on matter were patterns of sounds — not in air, of course, but in the sense of states of vibration of superstrings with a spin of 1. The 240 sequences associated with each note consist of 10 sets of 24 sequences, which correlate with the 24 gauge charges and their corresponding waves that travel around each whorl of the superstring. To every gauge charge corresponds a musical sequence, shaped according to the pattern of the tetractys, of 10 octaves of each note of the Pythagorean scale. Matter ultimately is a perfect harmony.
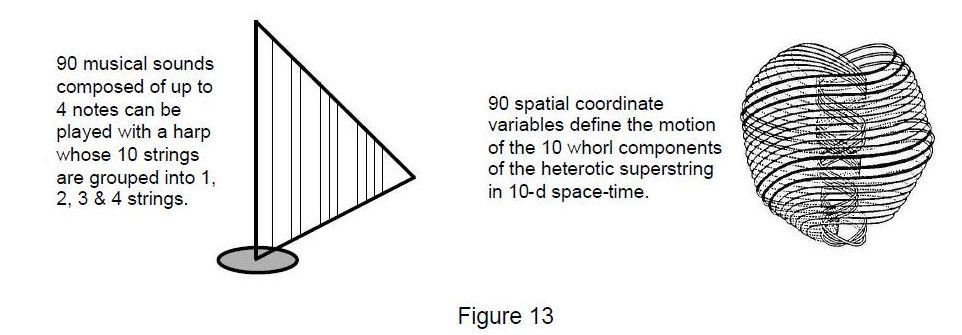
Additional evidence for the validity of this musical interpretation of the superstring is the fact that a tetractys of 10 notes can generate 90 harmonic and melodic intervals, chords and broken chords of up to four notes (3), whilst the 10 string-like, curves of the superstring need (10×9=90) spatial
15
coordinate variables to describe their motion in 10-dimensional space-time.* In other words, the heterotic superstring is like a 10-stringed harp or lyre (Fig. 13) whose range of musical sounds is defined by the sum (90) of integers making up the Platonic Lambda Tetractys — the very set of numbers whose relative proportions were discovered by the ancient Greeks to determine the tone ratios of the notes of the Pythagorean scale! As shown in reference 2, these 90 musical elements correlate with the 90 edges of the five Platonic solids. The Ideas of the Divine Mind manifest in time (music), space (Platonic solids) and space-time (superstrings) in analogous ways quantified by the same parameters.
If the musical analogy with superstring theory is correct, then the remaining (525–480=45) sequences of 4-7 sounds also require interpretation. There are two sets of sequences of seven sounds (one of 24, one of 12), six sequences of six sounds, two sequences of five sounds and one sequence of four sounds. Those other than the lattermost correspond to 44 yods on the boundaries (including the root edge) of some of the (7+7) enfolded polygons. The largest polygon — the dodecagon — has only 36 yods on its boundary, so a combination of polygons must be considered. They must be identical because a pair of dissimilar polygons would lead to an asymmetric distribution of the yods corresponding to the 480 sequences, which is, intuitively, unappealing. The only possible pair is the two octagons (Fig. 14). The two corners (
) of their root edge denote the two sequences of five sounds, the 12 (
) corners denote the 12 sequences of seven sounds and the 30 (o) yods denote the 30 sequences of either six or seven sounds. The 44 sequences must include four that correspond to all four yods of the root edge because no pair of similar polygons has 44 yods outside their root edge (4). This means that the 480 sequences correspond to the 288 yods inside the boundaries of the (7+7) polygons and to the 192 yods on the boundaries of all the polygons except the pair of octagons.
What is so special about an octagon? When its sectors are turned into tetractyses, its yod population is 49, which is the number value of EL ChAI, the Godname of Yesod. The pair of octagons has 90 yods outside their root edge and so they embody or
* In 11-d supergravity space-time the number 90 is the number of transverse coordinate variables of the 10 closed curves/whorls of the heterotic superstring of ordinary matter, the 10 coordinate variables measured along them corresponding to the 10 notes arranged as a tetractys.
16
generate the very archetypal number that we found (5) in the context of the Lambda Tetractys, the Platonic solids, the musical potential of a tetractys of 10 notes and the geometry of the heterotic superstring. Furthermore, a pair of separate, type B octagons has 240 yods surrounding their centres (6), so that they also embody this dynamical parameter of superstrings and its musical counterpart — the number of musical sequences playable with a tetractys of 10 notes. That the very polygon not involved in the encoding of the number 480 should define two numbers central to the musical analogy with superstrings is remarkable evidence of mathematical ‘Divine Design.’ Coincidence — the refuge of the sceptic — is implausible because it requires two fortuitous concurrences.
3. Conclusion
Although modern music uses the 13 notes of the tempered, chromatic scale, it originated in the West from the eight-note Pythagorean scale mathematically explained by Pythagoras. It is only the latter that can lay claim to have the universal validity of a law of nature as the modern musical scale is a human fabrication, a modification of the Pythagorean scale without any theoretical basis devised simply to increase the variety of tones available to the musician. Adhering to the earliest Greek traditions, many writers on speculative music theory have emphasized the ‘cosmic’ nature of the Pythagorean scale, pointing to its amazing, mathematical harmonies but offering little rational and scientific substantiation for this view, merely associations or correspondences with occult and religious ideas. Although this article, too, refers to a mystical tradition — Kabbalah — it makes striking quantitative connections with both a scientific theory and a body of information established over a hundred years ago that previous books (8) by the author have shown is profoundly consistent with established facts of nuclear and particle physics, as well as with still hypothetical ideas of this theory. This moves the present discussion from the tradition of metaphysical speculation and places it in the context of the world-wide search for an all-embracing ‘theory of everything.’ Popular books about superstrings often liken these vibrating strings to that of violin strings or piano wires. However, their authors never intend this comparison to be other than metaphorical. How could they, in view of the fact that the frequency range most common in music is about 500–4000 Hz, whereas superstrings may vibrate at up to 1043 Hz!? Nevertheless, such a huge difference in frequency does not imply that the mathematics of music is irrelevant to superstring theory. It indicates
17
only the obvious fact that the latter is not a branch of acoustics. This mathematics defines only relative, not absolute, pitches of sounds. Could it be, therefore, that an analogy relates the mathematics of music and superstring vibrations, one that makes their disparity in frequency irrelevant? Perhaps it is not accidental (9) that, just as musical tones group according to their pitch into sets of eight, so, too, eight mathematical objects (the so-called ‘zero and seven non-zero roots of the exceptional group E8’) define this mathematical group describing the symmetry of the unified force between heterotic superstrings. The parallel would exist because, as shown in reference 10, superstrings — like human beings — conform to the universal pattern of the “Image of God” blueprint, and so they must have mathematically analogous forms of communication, whether through sound waves in the case of humans or by exchanging virtual messenger particles when superstrings interact with one another. The heterotic superstring, which the author has shown (11) is the constituent of up and down quarks in atomic nuclei, is the microscopic Tree of Life and tetractys, its 10 whorls corresponding to the 10 Sephiroth of the former and to the 10 yods of the latter. The seven notes of the Pythagorean scale bear a formal correspondence to the seven Sephiroth of Construction that belong to the Tree of Life. These seven objective aspects of God appear in the subatomic world as the seven compactified dimensions of spacetime predicted by supergravity theory and in the heterotic superstring described by Besant & Leadbeater as the seven orders of spirillae making up each of its whorls (12), the six higher orders representing the winding of its string components about six of these dimensions curled up into one-dimensional circles (13). As Pythagoras discovered 2,500 years ago, the numbers 1, 2, 3, & 4 symbolised by the four rows of the tetractys express the relative pitches of the octave, perfect fourth and perfect fifth, leading to the beautiful, mathematical proportions of the notes of the musical Pythagorean scale. Similarly, the 10-fold, heterotic superstring of ordinary matter extends in 10 dimensions of space-time, both being manifestations of the universal mathematical paradigm of the tetractys governing holistic systems. Little wonder then that its forces and oscillatory form should turn out to be analogous to the musical sequences playable with tetractyses of ten octaves of each note of the Pythagorean scale!
References
1) Numbers in boldface are the number values of the Sephiroth in the four Worlds. They are calculated according to gematria, wherein the number
18
value of a word is the sum of the numbers assigned to its letters. They are listed in Table 2 below.
Table 2. Gematria number values of the Sephiroth in the four Worlds.
|
SEPHIRAH |
GODNAME |
ARCHANGEL |
ORDER OF |
MUNDANE |
|
| 1 | Kether (Crown) 620 |
EHYEH (I am) 21 |
Metatron (Angel of the Presence) 314 |
Chaioth ha Qadesh (Holy Living Creatures) 833 |
Rashith ha Gilgalim First Swirlings. (Primum Mobile) 636 |
| 2 | Chokmah (Wisdom) 73 |
YAHWEH, YAH (The Lord) 26, 15 |
Raziel (Herald of the Deity) 248 |
Auphanim (Wheels) 187 |
Masloth (The Sphere of the Zodiac) 140 |
| 3 | Binah (Understanding) 67 |
ELOHIM (God in multiplicity) 50 |
Tzaphkiel (Contemplation of God) 311 |
Aralim (Thrones) 282 |
Shabathai Rest. (Saturn) 317 |
| Daath (Knowledge) 474 |
|||||
| 4 | Chesed (Mercy) 72 |
EL (God) 31 |
Tzadkiel (Benevolence of God) 62 |
Chasmalim (Shining Ones) 428 |
Tzadekh Righteousness. (Jupiter) 194 |
| 5 | Geburah (Severity) 216 |
ELOHA (The Almighty) 36 |
Samael (Severity of God) 131 |
Seraphim (Fiery Serpents) 630 |
Madim Vehement Strength. (Mars) 95 |
| 6 | Tiphareth (Beauty) 1081 |
YAHWEH ELOHIM (God the Creator) 76 |
Michael (Like unto God) 101 |
Malachim (Kings) 140 |
Shemesh The Solar Light. (Sun) 640 |
| 7 | Netzach (Victory) 148 |
YAHWEH SABAOTH (Lord of Hosts) 129 |
Haniel (Grace of God) 97 |
Tarshishim or Elohim 1260 |
Nogah Glittering Splendour. (Venus) 64 |
| 8 | Hod (Glory) 15 |
ELOHIM SABAOTH (God of Hosts) 153 |
Raphael (Divine Physician) 311 |
Beni Elohim (Sons of God) 112 |
Kokab The Stellar Light. (Mercury) 48 |
| 9 | Yesod (Foundation) 80 |
SHADDAI EL CHAI (Almighty Living God) 49, 363 |
Gabriel (Strong Man of God) 246 |
Cherubim (The Strong) 272 |
Levanah The Lunar Flame. (Moon) 87 |
| 10 | Malkuth (Kingdom) 496 |
ADONAI MELEKH (The Lord and King) 65, 155 |
Sandalphon (Manifest Messiah) 280 |
Ashim (Souls of Fire) 351 |
Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth) 168 |
2) Article 12, p. 5.
5) The number of yods on the boundary of an n-sided, regular polygon divided into
19
tetractyses is 3n, that is, (3n–4) yods other than the four yods on one side. Two such enfolded polygons have (2(3n–4) = 6n – 8) yods outside their shared edge. But there is no integer solution for n in the equation: 6n – 8 = 44. Therefore, no pair of similar polygons can have 44 yods outside their shared edge.
6) Article 11, Section 2 & 3, and Article 12, Sections 4, 5 & 7.
7) An n-sided, regular polygon with its sectors each divided into three tetractyses (‘type B polygon’) has (15n+1) yods. A type B octagon has (15×8 + 1 = 121) yods, i.e., 120 yods surround its centre. Therefore, 240 yods surround the centres of two separate type B octagons.
8) Extra-sensory Perception of Quarks, Stephen M. Phillips (Theosophical Publishing House, Wheaton, Ill., USA, 1980); Anima: Remote Viewing of Subatomic Particles, Stephen M. Phillips (Theosophical Publishing House, Adyar, Chennai, India, 1996); ESP of Quarks and Superstrings, Stephen M. Phillips (New Age International, New Delhi, India, 1999).
9) Article 12, Section 8.
10) The Mathematical Connection between Religion and Science, Stephen M. Phillips (Antony Rowe Publishing, England, 2009).
12) Article 2, Section 2.
20