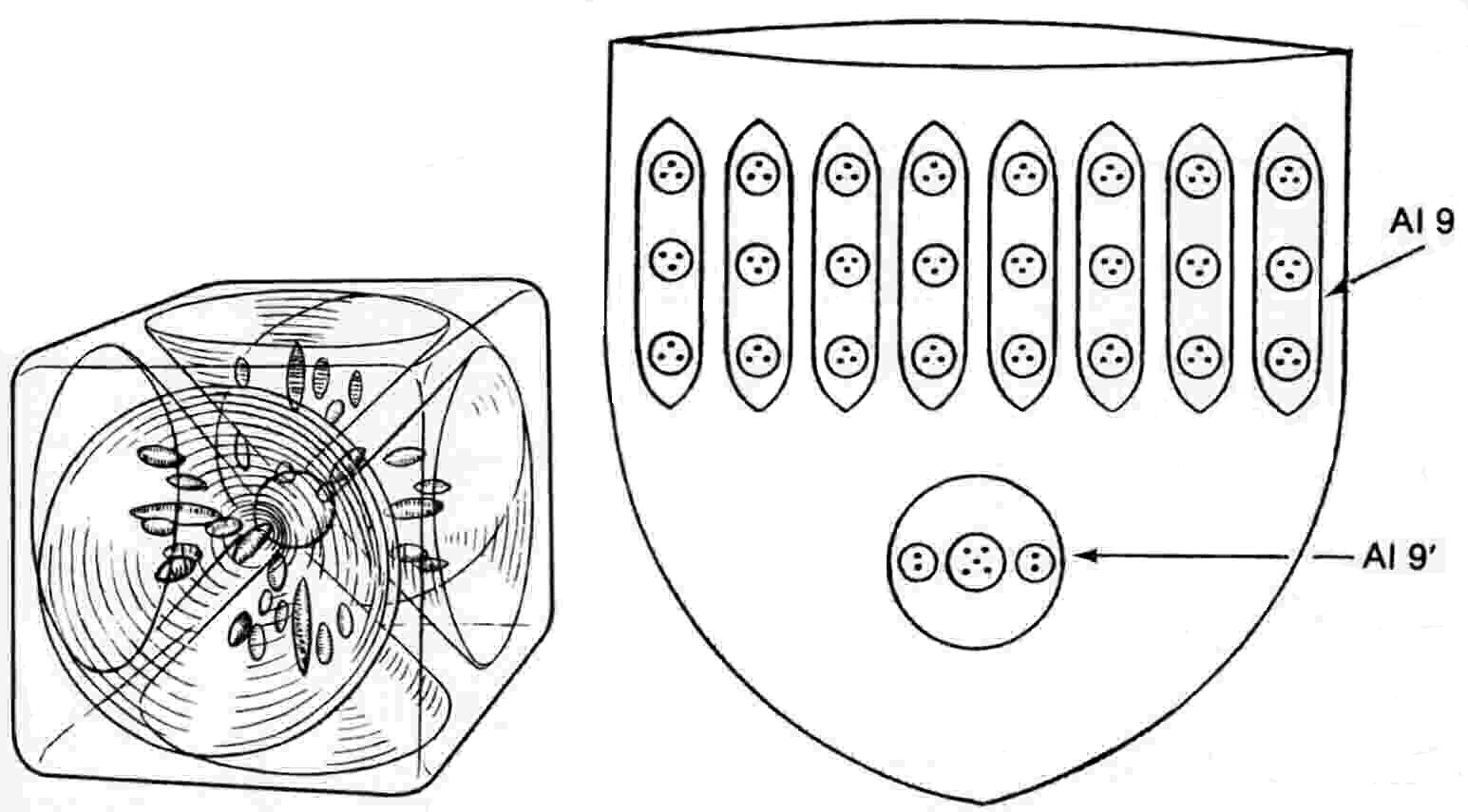
The Aluminium MPA

The aluminium MPA consists of six funnels directed towards the faces of an imaginary cube. Each funnel contains eight similar ovoids (Al9), each enclosing three spheres containing hydrogen triplets. Below these is an ovoid (Al9′) containing three spheres. Two spheres enclose duads of UPAs and the third encloses a group of five UPAs.
Aluminium MPA = 6(Al9′ + 8Al9).
The MPA is formed from two Al27 nuclei, which provide 486 subquarks — the same as the
number of UPAs. These comprise 242 X subquarks and 244 Y subquarks. The funnels cannot contain the same set of
particles because neither of these numbers is divisible exactly by 6. Seventy-two u quarks and seventy-two d quarks
are equally distributed among the six funnels, four groups of three per funnel. An Al9 group is either three u or
three d quarks bound together by the residual coupling between subquarks in each quark in
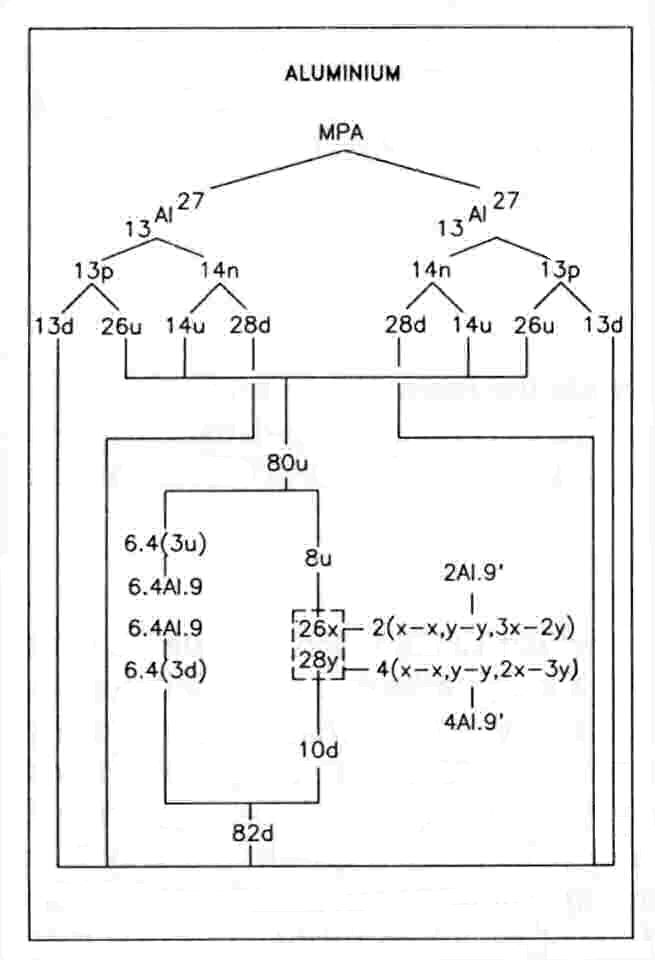
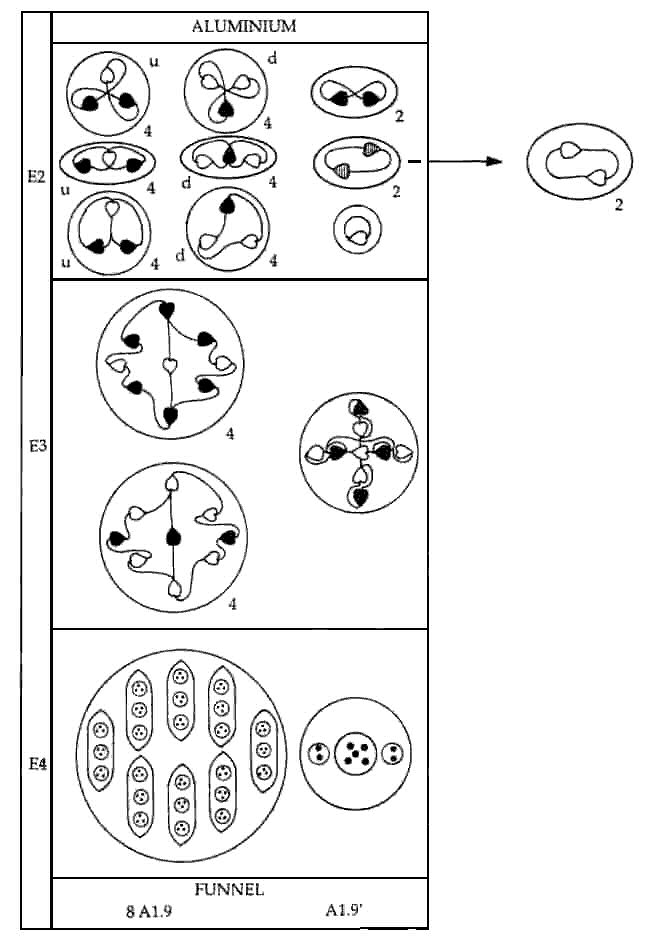
a way analogous to the nucleus holding together protons and neutrons in atomic nuclei. The disintegration diagram confirms the predictions that an Al9 is of two types, that there are four of each in a funnel and that they are u-u-u and d-d-d bound states. It shows that the eight Al9 groups separate at stage E3 into two types of sets of four, one type breaking up at stage E2 into three (+) triplets (u quarks), the other breaking up into three (−) triplets (d quarks).
The twenty-six X subquarks and twenty-eight Y subquarks making up two protons and four neutrons recombine, those in the protons forming an Al9′ group consisting of an X-X bound state, a Y-Y bound state and a 3X-2Y bound state:
proton (= u-u-d = 5X + 4Y) → X-X + Y-Y + 3X-2Y,
those in the neutron forming a Y-Y, an X-X and a 3Y-2X bound state:
neutron (= u-d-d = 4X + 5Y) → Y-Y + X-X + 3Y-2X.
Four of the Al9′ groups are thus the mirror states of the other two. The disintegration diagram depicts this group as breaking up at the E2 stage into a free UPA and four (+) duads (X-X). This disagrees with the prediction above, which requires the Al9′ to break up into a free UPA, two (+) duads and two (−) duads. But the disintegration diagram of the calcium MPA (see later), which also contains the Al9′ group, indicates that — as predicted — it is made up of a (+) duad and a (−) duad and that its group of five UPAs breaks up into two (0) duads and a UPA, so that it must contain at least two X subquarks and two Y subquarks. Suppose, however, that the two protons and four neutrons did not separately change into Al9′ groups but that, instead, their twenty-six X subquarks and twenty-eight Y subquarks regrouped so as to form n Al9′ groups (1≤n≤6) with the compositions:
X-X + X-X + 4X-(X or Y),
allowing them to break up into the four (+) duads (X-X) recorded for the aluminium MPA). Letting the (6−n) funnels contain A X subquarks and (9−A) Y subquarks (0≤A≤9), then, if the group of five UPAs in n funnels is 4X-X,
9n + (6−n)A = 26
and
(6−n)(9−A) = 28.
These equations have the single solution n = 2, A =2. If the group of five UPAs in n funnels is 4X-Y,
8n + (6−n)A = 26
and
n + (6−n)(9−A) = 28,
which simplifies to
(6−n)(9−A) = 22.
This has no solutions because 22 factorizes only as 2×11 and 11>(9−A) or (6−n) for all positive values of n and A. Two Al9′ groups can only have the composition:
X-X + X-X + 4X-X,
and the remaining four Al9′ groups can only have the composition:
X-X + Y-Y + 4Y-Y.
Presumably, Besant & Leadbeater examined only one of the two funnels predicted to contain Al9′ groups comprising two X-X bound states and a bound state of five X subquarks. Two similar groups of UPAs observed in different MPAs may be mirror states of each other, and therefore they need not necessarily have had the same subquark compositions unless the particles into which they disintegrated are indicated in the disintegration diagrams to be similar in either case. This is not the case for the aluminium and calcium MPAs.